题目内容
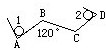 如图,一块半径为1厘米的圆板,从平面1的位置沿AB、BC、CD滚动到位置2.如果AB=BC=CD=10厘米,那么圆板滚过的面积是多少平方厘米?(π取3,保留小数点后面2位数字)
如图,一块半径为1厘米的圆板,从平面1的位置沿AB、BC、CD滚动到位置2.如果AB=BC=CD=10厘米,那么圆板滚过的面积是多少平方厘米?(π取3,保留小数点后面2位数字)分析:现将圆板滚过的图形分割成a、b、c、d、e、f、g,其中图a、b、c分别是长为9厘米、8厘米、7厘米,宽是2厘米的长方形;图d、f正好拼成一个圆;图e是半径为2厘米,圆心角为60°的扇形,恰好是圆面积的
;图g是3个边长为0.5厘米,厘米的小正方形与一个半径为0.5圆心角是90°的扇形面积之和.所以圆板滚过的图形面积为(9+8+7)×2+3×12+3×22×
+3×0.52×
=53.94.
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 4 |
解答:解:(9+8+7)×2+3×12+3×22×
+3×0.52×
,
=53.94(平方厘米).

答:圆板滚过的图形面积为53.94平方厘米.
| 1 |
| 6 |
| 1 |
| 4 |
=53.94(平方厘米).

答:圆板滚过的图形面积为53.94平方厘米.
点评:解答本题的关键在于想象出圆板滚过的图形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2009?河西区)如图,一个半径为1厘米的小圆盘沿着一个半径为4厘米的大圆盘外侧做无滑动的滚动.当小圆盘的中心围绕大圆盘中心转动90度后,小圆盘运动过程中扫过的面积是多少平方厘米?
(2009?河西区)如图,一个半径为1厘米的小圆盘沿着一个半径为4厘米的大圆盘外侧做无滑动的滚动.当小圆盘的中心围绕大圆盘中心转动90度后,小圆盘运动过程中扫过的面积是多少平方厘米? 如图,一个半径为1厘米的圆沿着一个直角三角形的三边滚动一周,那么这个圆的圆心所经过的总路程为
如图,一个半径为1厘米的圆沿着一个直角三角形的三边滚动一周,那么这个圆的圆心所经过的总路程为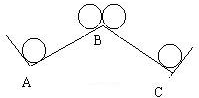 如图,一块半径为1厘米的圆板,从平面A的位置沿AB、BC滚动到位置C.如果AB=BC=10厘米,角ABC=120°.那么圆板滚过的面积是多少平方厘米?(π取3,保留小数点后面两位数字)
如图,一块半径为1厘米的圆板,从平面A的位置沿AB、BC滚动到位置C.如果AB=BC=10厘米,角ABC=120°.那么圆板滚过的面积是多少平方厘米?(π取3,保留小数点后面两位数字) 如图,一个半径为1厘米的小圆盘沿着一个半径为4厘米的大圆盘外侧做无滑动的滚动.当小圆盘的中心围绕大圆盘中心转动90度后,小圆盘运动过程中扫过的面积是多少平方厘米?
如图,一个半径为1厘米的小圆盘沿着一个半径为4厘米的大圆盘外侧做无滑动的滚动.当小圆盘的中心围绕大圆盘中心转动90度后,小圆盘运动过程中扫过的面积是多少平方厘米?