题目内容
如图△ABC、△ACD、△ADE、△AEF都是等腰直角三角形，如果AB=2，那么封闭多边形ABCDEF的面积S= ．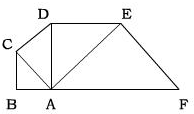
分析：因为等腰直角三角形的面积等于直角边的平方除以2，于是求出每个等腰直角三角形的直角边的平方值，即可分别求出每个等腰直角三角形的面积，从而问题逐步得解．
解答：解：三角形ABC的面积为22÷2=2，
三角形ACD的面积为：8÷2=4，
三角形ADE的面积为16÷2=8，
三角形AEF的面积为32÷2=16，
所以封闭多边形ABCDEF的面积S=2+4+8+16=30；
故答案为：30．
三角形ACD的面积为：8÷2=4，
三角形ADE的面积为16÷2=8，
三角形AEF的面积为32÷2=16，
所以封闭多边形ABCDEF的面积S=2+4+8+16=30；
故答案为：30．
点评：解答此题的主要依据是：等腰直角三角形的面积等于直角边的平方除以2，以及勾股定理的灵活应用．
练习册系列答案
小题狂做系列答案
相关题目
（2008?常熟市）如图，方格纸的每个小方格的边长都是1的正方形，A，B两点在小方格的顶点上，A点的位置可以用（1，1）表示；B点的位置可用（2，3）表示．现在要在小方格的顶点上找到C点，连接AB，AC和BC后得三角形，且三角形ABC的面积为2．请你找出5个符合条件的C点，并在下面用数对表示出各点的位置．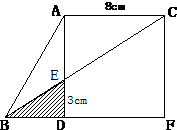
如图，已知三角形ABC的面积是36平方厘米，AC长8厘米，DE长3厘米，求阴影部分的面积．
如图，三角形ABC的面积是15平方厘米，D是AC的中点，F点在BC上，且CF=2BF，AF与BD相交于点E．那么，四边形CDEF的面积是
如图，在△ABC中，已知M、N分别在AC、BC上，BM与AN相交与O．若△AOM，△ABO和△OBN的面积分别是3、2、1．求△MNC的面积．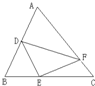
在如图△ABC中，AD=
AB，BE=
BC，CF=
AC．如果△DEF的面积是1，那么△ABC的面积是
