题目内容
 如图,在△ABC中,已知M、N分别在AC、BC上,BM与AN相交与O.若△AOM,△ABO和△OBN的面积分别是3、2、1.求△MNC的面积.
如图,在△ABC中,已知M、N分别在AC、BC上,BM与AN相交与O.若△AOM,△ABO和△OBN的面积分别是3、2、1.求△MNC的面积.分析:根据同高三角形的面积比等于对应底的比,即可得
=
=
,由S△OMA=3,S△OAB=2,S△OBN=1,即可求得△OMN的面积,然后设S△CMN=x,由
=
=
,利用方程即可求得S△CMN的值.
| S△OMN |
| S△OBN |
| OM |
| OB |
| S△OMA |
| S△OBA |
| S△ABN |
| S△ANC |
| S△MBN |
| S△MNC |
| BN |
| NC |
解答:解:因为
=
=
,
∴S△OMN=
,由S△OBN=
×1=
,
设S△CMN=x,
∵由
=
=
,
∴
=
,
解得x=
,
即S△CMN=22.5.
答:△MNC的面积是22.5.
| S△OMN |
| S△OBN |
| OM |
| OB |
| S△OMA |
| S△OBA |
∴S△OMN=
| S△OMA |
| S△OBA |
| 3 |
| 2 |
| 3 |
| 2 |
设S△CMN=x,
∵由
| S△ABN |
| S△ANC |
| S△MBN |
| S△MNC |
| BN |
| NC |
∴
| 2+1 | ||
3+
|
| ||
| X |
解得x=
| 45 |
| 2 |
即S△CMN=22.5.
答:△MNC的面积是22.5.
点评:此题考查了面积与等积变换的知识.此题难度较大,解题的关键是掌握同高三角形的面积比等于对应底的比性质的应用,注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 如图,在△ABC中,D为BC边上任一点,AE=
如图,在△ABC中,D为BC边上任一点,AE= 如图,在△ABC中,两条角平分线CD、EF相交于F,∠A=60°,则∠DFE=
如图,在△ABC中,两条角平分线CD、EF相交于F,∠A=60°,则∠DFE= (2013?北京模拟)如图,在△ABC中,AD=
(2013?北京模拟)如图,在△ABC中,AD= 如图,在△ABC中,E、D、F分别为AD、BC、AB的中点,BD=DE=EC,BF=FA,△EDF的面积是1,那么△ABC的面积是多少?
如图,在△ABC中,E、D、F分别为AD、BC、AB的中点,BD=DE=EC,BF=FA,△EDF的面积是1,那么△ABC的面积是多少?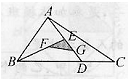 如图,在△ABC中,
如图,在△ABC中,