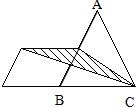
题目内容
 如图,三角形ABC的面积是15平方厘米,D是AC的中点,F点在BC上,且CF=2BF,AF与BD相交于点E.那么,四边形CDEF的面积是
如图,三角形ABC的面积是15平方厘米,D是AC的中点,F点在BC上,且CF=2BF,AF与BD相交于点E.那么,四边形CDEF的面积是6.25
6.25
平方厘米.分析:由于D为AC的中点,因此三角形BDC的面积是三角形面积的一半,取FC的中点,连结DG,又由已知条件可知,DG是三角形BDG的中位线,EF是三角形BDG的中位线,BF=FG=GC,因此三角形DGC的面积是三角形BDC面积的
,从而求出三角形DGC的面积,三角形BEF面积是三角形面积的
,进而求得三角形BEF的面积,三角形BDG的面积减去三角形BEF的面积就是四边形CDEF的面积.
| 1 |
| 3 |
| 1 |
| 4 |
解答:解:如图,取CF中点G 连接DG
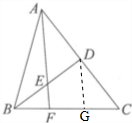
因为D为AC的中点 所以△BCD面积=
平方厘米,
因为D是AC的中点,G是CF的中点,
所以 DG可知为△ACF中位线
因此DG∥AF,
由于EF是AF的一部分,
所以DG∥EF
又因为 G为CF中点 且CF=2BF
所以 BF=FG=GC,
因此EF为△BDG 中位线
所以△BEF面积=△BDG面积的
,且△BDG的面积=2△DGC的面积
所以 3△DGC面积=△BCD面积=
平方厘米,
所以△DGC的面积=
÷3=
(平方厘米)
△BDG面积=
-
=5(平方厘米),△BEF面积5÷4=
(平方厘米)
因此 四边形CDEF的面积=△BDC面积-△BEF面积
-
=
=6.25(平方厘米);
故答案为:6.25

因为D为AC的中点 所以△BCD面积=
| 15 |
| 2 |
因为D是AC的中点,G是CF的中点,
所以 DG可知为△ACF中位线
因此DG∥AF,
由于EF是AF的一部分,
所以DG∥EF
又因为 G为CF中点 且CF=2BF
所以 BF=FG=GC,
因此EF为△BDG 中位线
所以△BEF面积=△BDG面积的
| 1 |
| 4 |
所以 3△DGC面积=△BCD面积=
| 15 |
| 2 |
所以△DGC的面积=
| 15 |
| 2 |
| 5 |
| 2 |
△BDG面积=
| 15 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
因此 四边形CDEF的面积=△BDC面积-△BEF面积
| 15 |
| 2 |
| 5 |
| 4 |
| 25 |
| 4 |
故答案为:6.25
点评:本题通过作辅助线,利用三角形中位线定理等知识求出三角形BEF的面积,进而求出四边形CDEF的面积.

练习册系列答案
相关题目
 如图,三角形ABC的面积是16,D是AC的中点,E是BD的中点,那四边形CDEF的面积是多少?
如图,三角形ABC的面积是16,D是AC的中点,E是BD的中点,那四边形CDEF的面积是多少? 如图,三角形ABC的面积为10,AD与BF交于点E,且AE=ED,BD=
如图,三角形ABC的面积为10,AD与BF交于点E,且AE=ED,BD= 如图,三角形ABC的面积是240平方厘米,D是AC的中点,E是BC的三等分点,则阴影部分的面积=
如图,三角形ABC的面积是240平方厘米,D是AC的中点,E是BC的三等分点,则阴影部分的面积= 如图,三角形ABC的面积是20平方厘米,求阴影部分的面积.
如图,三角形ABC的面积是20平方厘米,求阴影部分的面积.