题目内容
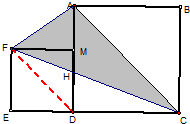 如图已知正方形ABCD和正方形DEFM,且正方形ABCD的边长为8分米.请问图中阴影部分的面积是多少平方分米?
如图已知正方形ABCD和正方形DEFM,且正方形ABCD的边长为8分米.请问图中阴影部分的面积是多少平方分米?
解:连结FD.
S△AFD= ×AD×FM,
×AD×FM,
S△FDC= ×DC×FE,
×DC×FE,
由于AD=DC,FG=FE,
所以S△AFD=S△FDC,
而△FHD是它们的公共部分,因此,△AHD与△HCD的面积相等,
可得S△AFC=S△AHC+S△HCD=S△ADC= S正方形ABCD=
S正方形ABCD= ×64=32(平方分米).
×64=32(平方分米).
答:图中阴影部分的面积是32平方分米.
分析:连结FD.根据等底等高的三角形面积相等可得S△AFD=S△FDC,而△FHD是它们的公共部分,因此,△AHD与△HCD的面积相等,从而得到S△AFC=S△AHC+S△HCD=S△ADC= S正方形ABCD,依此即可求解.
S正方形ABCD,依此即可求解.
点评:考查了三角形面积,注意等底等高的三角形面积相等,依此得到图中阴影部分的面积是 S正方形ABCD.
S正方形ABCD.
S△AFD=
 ×AD×FM,
×AD×FM,S△FDC=
 ×DC×FE,
×DC×FE,由于AD=DC,FG=FE,
所以S△AFD=S△FDC,
而△FHD是它们的公共部分,因此,△AHD与△HCD的面积相等,
可得S△AFC=S△AHC+S△HCD=S△ADC=
 S正方形ABCD=
S正方形ABCD= ×64=32(平方分米).
×64=32(平方分米).答:图中阴影部分的面积是32平方分米.
分析:连结FD.根据等底等高的三角形面积相等可得S△AFD=S△FDC,而△FHD是它们的公共部分,因此,△AHD与△HCD的面积相等,从而得到S△AFC=S△AHC+S△HCD=S△ADC=
 S正方形ABCD,依此即可求解.
S正方形ABCD,依此即可求解.点评:考查了三角形面积,注意等底等高的三角形面积相等,依此得到图中阴影部分的面积是
 S正方形ABCD.
S正方形ABCD. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图直角三角形ABC中,已知AB=21厘米,BC=28厘米,如果在这个直角三角形中作一个尽量大的正方形,那么这个正方形的面积是
如图直角三角形ABC中,已知AB=21厘米,BC=28厘米,如果在这个直角三角形中作一个尽量大的正方形,那么这个正方形的面积是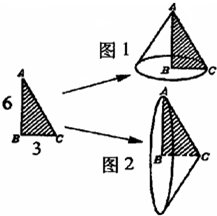
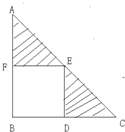 如图,在直角三角形ABC中有一个正方形BDEF,E点正好落在直角三角形的斜边AC上,已知AE=10厘米,EC=8厘米,则阴影部分的面积是多少平方厘米?
如图,在直角三角形ABC中有一个正方形BDEF,E点正好落在直角三角形的斜边AC上,已知AE=10厘米,EC=8厘米,则阴影部分的面积是多少平方厘米? 如图,在直角三角形ABC中有一个正方形BDEF,E点正好落在直角三角形的斜边AC上,已知AE=8厘米,EC=10厘米,那么图中阴影部分的面积是多少平方厘米?
如图,在直角三角形ABC中有一个正方形BDEF,E点正好落在直角三角形的斜边AC上,已知AE=8厘米,EC=10厘米,那么图中阴影部分的面积是多少平方厘米? 如图是一个由两个正方形拼合而成的图形,它们的边长分别是m厘米及n厘米,且CDE为一直线.已知m和n都是两位数,且m2=2n.若三角形ABC的面积等于a平方厘米,求a的最大值.
如图是一个由两个正方形拼合而成的图形,它们的边长分别是m厘米及n厘米,且CDE为一直线.已知m和n都是两位数,且m2=2n.若三角形ABC的面积等于a平方厘米,求a的最大值.