题目内容
 如图是一个由两个正方形拼合而成的图形,它们的边长分别是m厘米及n厘米,且CDE为一直线.已知m和n都是两位数,且m2=2n.若三角形ABC的面积等于a平方厘米,求a的最大值.
如图是一个由两个正方形拼合而成的图形,它们的边长分别是m厘米及n厘米,且CDE为一直线.已知m和n都是两位数,且m2=2n.若三角形ABC的面积等于a平方厘米,求a的最大值.分析:由“m2=2n”可得n=m×m÷2,然后运用假设法,求出大小正方形的边长,解决问题.
解答:解:n=m×m÷2,
假设m=15,则15×15÷2>100,故舍去;
设m=14,则14×14÷2=98,符合题意.
因此大小正方形的边长分别为98cm及14cm.
故三角形ABC的面积是14×14÷2=98(平方厘米).
答:a的最大值98.
假设m=15,则15×15÷2>100,故舍去;
设m=14,则14×14÷2=98,符合题意.
因此大小正方形的边长分别为98cm及14cm.
故三角形ABC的面积是14×14÷2=98(平方厘米).
答:a的最大值98.
点评:此题解答的关键在于运用假设法,求出大小正方形的边长.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 如图.一大一小两个正方形拼在一起,若阴影部分的面积是10,能否求出大正方形的面积?若能求出,请写出计算过程;若不能求出,请说明理由.
如图.一大一小两个正方形拼在一起,若阴影部分的面积是10,能否求出大正方形的面积?若能求出,请写出计算过程;若不能求出,请说明理由.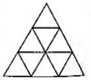 如图是一个由9个相同的小等边三角形所组成的大等边三角形.现在要把一枚黑子和一枚白子分别被放入两个小等边三角形中,并且要求这两个小等边三角形既没有公共边也没有公共顶点,那么共有
如图是一个由9个相同的小等边三角形所组成的大等边三角形.现在要把一枚黑子和一枚白子分别被放入两个小等边三角形中,并且要求这两个小等边三角形既没有公共边也没有公共顶点,那么共有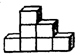 (2011?建华区)如图是一个由8个相同的小正方体组成的立体图形,从右面看到形状应该是( )
(2011?建华区)如图是一个由8个相同的小正方体组成的立体图形,从右面看到形状应该是( )