题目内容
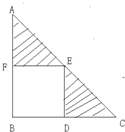如图，在直角三角形ABC中有一个正方形BDEF，E点正好落在直角三角形的斜边AC上，已知AE=10厘米，EC=8厘米，则阴影部分的面积是多少平方厘米？分析：如图，由于BDEF是正方形，因此EF=ED，∠DEF=90°，三角形AFE绕点E逆时针旋转90°，与三角形EDC组成一个直角三角形，直角边分别是10厘米、8厘米，由此即可求出阴影部分的面积．
解答：解：如图，
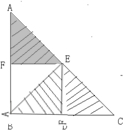
三角形AFE绕点E逆时针旋转90°，与三角形EDC组成一个直角三角形，两直角边分别是10厘米、8厘米，
其面积是：
×10×8=40（平方厘米）；
故答案为：40平方厘米．
三角形AFE绕点E逆时针旋转90°，与三角形EDC组成一个直角三角形，两直角边分别是10厘米、8厘米，
其面积是：
| 1 |
| 2 |
故答案为：40平方厘米．
点评：解答此题的关键是巧妙地把阴影部分三角形AFE绕点E逆时针旋转90°，与阴影部分三角形EDC组成一个直角三角形．
练习册系列答案
相关题目
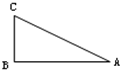如图：在直角三角形中，∠A=28°，∠C=
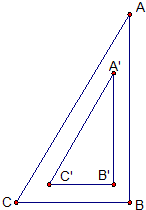如图，在直角三角形ABC中，∠ABC=90°，ABPA′B′，BCPB′C′，ACPA′C′，且三对平行线的距离都是1，若AC=10，AB=8，BC=6，求三角形A′B′C′上的点到三角形ABC三边距离的最大值．
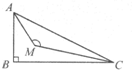如图，在直角三角形ABC中，AM、CM分别平分∠A、∠C，则∠M是
如图：在直角三角形中，∠A=28°，∠C=________°．