题目内容
 如图直角三角形ABC中,已知AB=21厘米,BC=28厘米,如果在这个直角三角形中作一个尽量大的正方形,那么这个正方形的面积是
如图直角三角形ABC中,已知AB=21厘米,BC=28厘米,如果在这个直角三角形中作一个尽量大的正方形,那么这个正方形的面积是144
144
平方厘米.分析:以直角三角形ABC的直角顶点为正方形的顶点,正方形的两边在直角三角形ABC的直角边上是三角形中最大的正方形,可设正方形的边长为x厘米,可得比例式x:28=(21-x):21,依此可得正方形的边长,再根据正方形的面积公式列式求解即可.
解答: 解:设正方形的边长为x厘米,则
解:设正方形的边长为x厘米,则
x:28=(21-x):21,
21x=28(21-x),
21x=28×21-28x,
21x+28x=588,
49x=588,
x=12.
12×12=144(平方厘米).
答:这个正方形的面积是144平方厘米.
故答案为:144.
 解:设正方形的边长为x厘米,则
解:设正方形的边长为x厘米,则x:28=(21-x):21,
21x=28(21-x),
21x=28×21-28x,
21x+28x=588,
49x=588,
x=12.
12×12=144(平方厘米).
答:这个正方形的面积是144平方厘米.
故答案为:144.
点评:考查了正方形的面积问题.在直角三角形中作一个尽量大的正方形,关键是列出比例式求得正方形的边长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
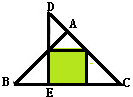 (2013?北京模拟)如图,三角形ABC和三角形DEC都是等腰直角三角形,A和E是直角等点,阴影部分是正方形.如果三角形DEC的面积是24平方米,那么三角形ABC的面积是
(2013?北京模拟)如图,三角形ABC和三角形DEC都是等腰直角三角形,A和E是直角等点,阴影部分是正方形.如果三角形DEC的面积是24平方米,那么三角形ABC的面积是 如图直角三角形ABC,以BC为轴旋转一周,得到一个立体图形,求这个立体图形的体积.
如图直角三角形ABC,以BC为轴旋转一周,得到一个立体图形,求这个立体图形的体积.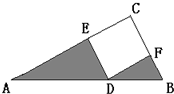 如图,三角形ABC是直角三角形,四边形EDFC是正方形,两个阴影三角形的面积之和是32平方厘米,AD:DB=4:1,求AD的长度.
如图,三角形ABC是直角三角形,四边形EDFC是正方形,两个阴影三角形的面积之和是32平方厘米,AD:DB=4:1,求AD的长度. 如图直角三角形ABC,以BC为轴旋转一周,得到一个立体图形,求这个立体图形的体积.
如图直角三角形ABC,以BC为轴旋转一周,得到一个立体图形,求这个立体图形的体积.