题目内容
 如图,三角形ABC的面积为10,AD与BF交于点E,且AE=ED,BD=
如图,三角形ABC的面积为10,AD与BF交于点E,且AE=ED,BD=| 2 | 3 |
分析:连接DF,因为AE=DE,△AEF的面积=△EDF的面积,△ABE的面积=△BDE的面积.因为BD=
BC,所以△BDF的面积=△DCF的面积×2,因此△ABF的面积=△BDF的面积=△DCF的面积×2;所以△ABC的面积=△DCF的面积×5,于是△DCF的面积=10÷5=2(平方厘米).阴影部分面积等于△BDF的面积=△DCF的面积×2=2×2=4(平方厘米).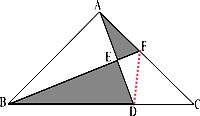
| 2 |
| 3 |

解答:解:连接DF,
则S△DCF的面积=10÷5=2(平方厘米).
阴影部分面积等于△BDF的面积=△DCF的面积×2=2×2=4(平方厘米);
答:阴影部分的总面积是4平方厘米.
则S△DCF的面积=10÷5=2(平方厘米).
阴影部分面积等于△BDF的面积=△DCF的面积×2=2×2=4(平方厘米);
答:阴影部分的总面积是4平方厘米.
点评:解答此题的关键是先连接DF,然后根据三角形面积和比的正比关系进行分析,进而得出结论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,三角形ABC的面积是16,D是AC的中点,E是BD的中点,那四边形CDEF的面积是多少?
如图,三角形ABC的面积是16,D是AC的中点,E是BD的中点,那四边形CDEF的面积是多少?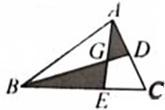 如图,三角形ABC的面积是240平方厘米,D是AC的中点,E是BC的三等分点,则阴影部分的面积=
如图,三角形ABC的面积是240平方厘米,D是AC的中点,E是BC的三等分点,则阴影部分的面积= 如图,三角形ABC的面积是20平方厘米,求阴影部分的面积.
如图,三角形ABC的面积是20平方厘米,求阴影部分的面积.