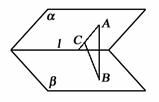
99. 已知:如图,平面a ∩平面b =直线l,A∈a ,AB⊥b ,B∈b ,BC⊥a ,C∈a,求证:AC⊥l.
证明:∵ AB⊥b ,l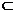 b
b
∴ l⊥AB
∵ BC⊥a ,l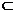 a
a
 ∴ l⊥BC
∴ l⊥BC
∵ AB∩BC=B
∴ l⊥平面ABC
∵ AC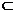 平面ABC
平面ABC
∴ l⊥AC
100. 已知:如图,P
98. 求证:MN⊥AB. 解析:连结MB、MA,证明MB=MA.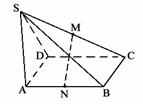 已知ABCD是矩形,SA⊥平面ABCD,M、N分别是SC、AB的中点.
已知ABCD是矩形,SA⊥平面ABCD,M、N分别是SC、AB的中点.
99. 已知:如图,平面a ∩平面b =直线l,A∈a ,AB⊥b ,B∈b ,BC⊥a ,C∈a,求证:AC⊥l.
证明:∵ AB⊥b ,l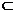 b
b
∴ l⊥AB
∵ BC⊥a ,l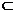 a
a
 ∴ l⊥BC
∴ l⊥BC
∵ AB∩BC=B
∴ l⊥平面ABC
∵ AC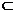 平面ABC
平面ABC
∴ l⊥AC
100. 已知:如图,P
98. 求证:MN⊥AB. 解析:连结MB、MA,证明MB=MA. 已知ABCD是矩形,SA⊥平面ABCD,M、N分别是SC、AB的中点.
已知ABCD是矩形,SA⊥平面ABCD,M、N分别是SC、AB的中点.