2.已知函数 ,
, .求
.求 的单调区间和值域.
的单调区间和值域.
学习笔记
教师备课
学习笔记
教师备课
学习笔记
教师备课
学习笔记
1.3.2利用导数研究函数的极值
(第二课时)
|
学习目标: ⒈理解函数的最大值和最小值的概念,掌握可导函数  在闭区间 在闭区间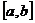 上所有点(包括端点 上所有点(包括端点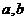 )处的函数中的最大(或最小)值必有的充分条件; )处的函数中的最大(或最小)值必有的充分条件;⒉掌握用导数求函数的极值及最值的方法和步骤 学习重点难点: 利用导数求函数的最大值和最小值的方法. 自主学习 一、知识再现: 求可导函数f(x)的极值的步骤: (1)确定函数的定义区间,求导数f′(x)  (2)求方程f′(x)=0的根  (3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查f′(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右不改变符号,那么f(x)在这个根处无极值  二、新课探究 1、函数的最大值和最小值 观察图中一个定义在闭 区间 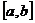 上的函数 上的函数 的 的图象.图中 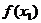 与 与 是 是极小值,  是极大值.函 是极大值.函数  在 在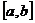 上的最大值 上的最大值 是 是 ,最小值是 ,最小值是 . .一般地,在闭区间 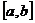 上连续的函数 上连续的函数 在 在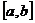 上必有最大值 上必有最大值与最小值. 说明:⑴在开区间 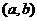 内连续的函数 内连续的函数 不一定有最大值与最小值.如函数 不一定有最大值与最小值.如函数 在 在 内连续,但没有最大值与最小值; 内连续,但没有最大值与最小值;⑵函数的最值是比较整个定义域内的函数值得出的;函数的极值是比较极值点附近函数值得出的. ⑶函数  在闭区间 在闭区间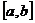 上连续,是 上连续,是 在闭区间 在闭区间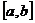 上有最大值与最小值的充分条件而非必要条件. 上有最大值与最小值的充分条件而非必要条件.(4)函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个  2、利用导数求函数的最值步骤: 由上面函数  的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进行比较,就可以得出函数的最值了. 的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进行比较,就可以得出函数的最值了.设函数  在 在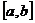 上连续,在 上连续,在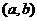 内可导,则求 内可导,则求 在 在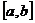 上的最大值与最小值的步骤如下: 上的最大值与最小值的步骤如下:⑴求  在 在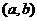 内的极值; 内的极值;⑵将  的各极值与 的各极值与 、 、 比较得出函数 比较得出函数 在 在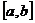 上的最值 上的最值 三、例题解析: 例1求函数  在区间 在区间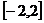 上的最大值与最小值 上的最大值与最小值 解:先求导数,得 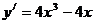 令  =0即 =0即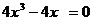 解得 解得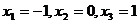 导数  的正负以及 的正负以及 , , 如下表 如下表
从上表知,当 值4 例2
已知
函数,在[1,+∞)上是增函数;(2) 出 解:设g(x)= 在[1,+∞)上是增函数 ∴g(x)在(0,1)上是减函数,在[1,+∞)上是增函数. ∴ 经检验,a=1,b=1时,f(x)满足题设的两个条件. 课堂巩固: 0 445720 445728 445734 445738 445744 445746 445750 445756 445758 445764 445770 445774 445776 445780 445786 445788 445794 445798 445800 445804 445806 445810 445812 445814 445815 445816 445818 445819 445820 445822 445824 445828 445830 445834 445836 445840 445846 445848 445854 445858 445860 445864 445870 445876 445878 445884 445888 445890 445896 445900 445906 445914 447090 |

 ;(2)若
;(2)若 ,求
,求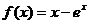 在
在 上的最大值是________;最小值是_______.
上的最大值是________;最小值是_______.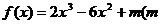 为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值为
.
为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值为
.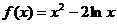 的最小值是( )
的最小值是( )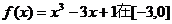 上的最大值,最小值分别是( )
上的最大值,最小值分别是( )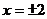 时,函数有最大值13,当
时,函数有最大值13,当 时,函数有最小
时,函数有最小 ,
, ∈(0,+∞).是否存在实数
∈(0,+∞).是否存在实数 ,使
,使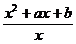 ∵f(x)在(0,1)上是减函数,
∵f(x)在(0,1)上是减函数, ∴
∴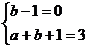 解得
解得
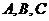 的对边分别为
的对边分别为 且
且 成等差数列.
成等差数列.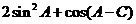 的范围.
的范围.