17.一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为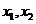 ,记
,记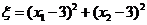 .
.
(1)分别求出 取得最大值和最小值时的概率;
取得最大值和最小值时的概率;
(2)求 的分布列及数学期望.
的分布列及数学期望.
解:(1)掷出点数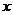 可能是:
可能是: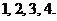
则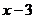 分别得:
分别得: 于是
于是 的所有取值分别为:
的所有取值分别为: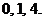
因此 的所有取值为:0,1,2,4,5,8.
的所有取值为:0,1,2,4,5,8.
当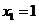 且
且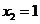 时,
时,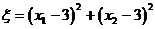 可取得最大值
可取得最大值 ,
,
此时,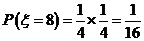 ;
;
当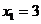 且
且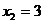 时,
时,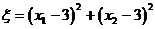 可取得最小值
可取得最小值 .
.
此时,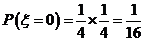 .
.
(2)由(Ⅰ)知 的所有取值为:0,1,2,4,5,8.
的所有取值为:0,1,2,4,5,8.
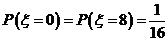 ;
;
当 =1时,
=1时,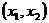 的所有取值为(2,3)、(4,3)、(3,2)、(3,4).即
的所有取值为(2,3)、(4,3)、(3,2)、(3,4).即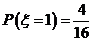 ;
;
当 =2时,
=2时,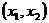 的所有取值为(2,2)、(4,4)、(4,2)、(2,4).
的所有取值为(2,2)、(4,4)、(4,2)、(2,4).
即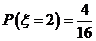 ;
;
当 =4时,
=4时,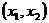 的所有取值为(1,3)、(3,1).即
的所有取值为(1,3)、(3,1).即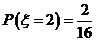 ;
;
当 =5时,
=5时,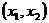 的所有取值为(2,1)、(1,4)、(1,2)、(4,1).即
的所有取值为(2,1)、(1,4)、(1,2)、(4,1).即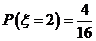 .
.
所以ξ的分布列为:
|
ξ |
0 |
1 |
2 |
4 |
5 |
8 |
|
P |
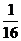 |
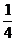 |
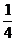 |
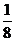 |
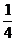 |
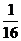 |
18
已知函数 .
.
(Ⅰ)若函数 在
在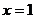 处取得极值,且曲线
处取得极值,且曲线 在点
在点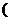
 ,
,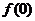
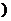 处的切线与直线
处的切线与直线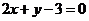 平行,求
平行,求 的值;
的值;
(Ⅱ)若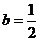 ,试讨论函数
,试讨论函数 的单调性.
的单调性.
解:(Ⅰ)函数 的定义域为
的定义域为 .
.

由题意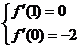 ,解得
,解得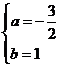
 .
.
(Ⅱ)若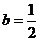 , 则
, 则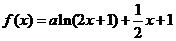 .
.
 .
.
(1)令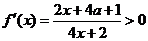 ,由函数定义域可知,
,由函数定义域可知, ,所以
,所以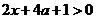
①当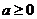 时,
时, ,
,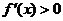 ,函数
,函数 单调递增;
单调递增;
②当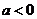 时,
时,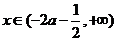 ,
,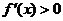 ,函数
,函数 单调递增;
单调递增;
(2)令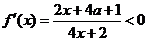 ,即
,即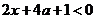
①当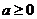 时,不等式
时,不等式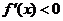 无解;
无解;
②当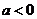 时,
时,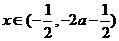 ,
,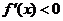 ,函数
,函数 单调递减;
单调递减;
综上:当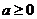 时,函数
时,函数 在区间
在区间 为增函数;
为增函数;
当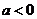 时,函数
时,函数 在区间
在区间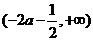 为增函数;
为增函数;
在区间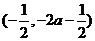 为减函数.
为减函数.
 如图所示,S1、S2是两个相干波源,它们振动同步且振幅相同。实线和虚线分别表示在某一时刻它们所发出的波的波峰和波谷。关于图中所标的a、b、c、d四点,下列说法中正确的有( )
如图所示,S1、S2是两个相干波源,它们振动同步且振幅相同。实线和虚线分别表示在某一时刻它们所发出的波的波峰和波谷。关于图中所标的a、b、c、d四点,下列说法中正确的有( ) 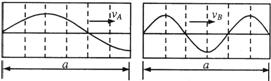 A.1:3 B.1:2
A.1:3 B.1:2
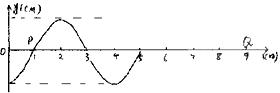
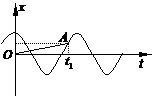 一个质点做简谐运动,它的振动图象如图,则(
)
一个质点做简谐运动,它的振动图象如图,则(
)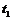 时间内的位移
时间内的位移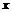 轴的投影是质点在
轴的投影是质点在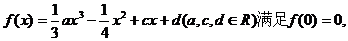 已知函数
已知函数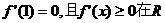 上恒成立
上恒成立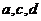 的值;
的值;
 上有最小值-5?若
上有最小值-5?若
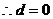
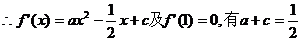
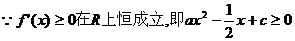 恒成立
恒成立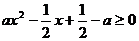 恒成立
恒成立 时,上式不能恒成立
时,上式不能恒成立 是二次函数
是二次函数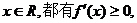 于是由二次函数的性质可得
于是由二次函数的性质可得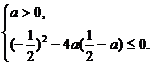 即
即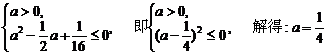
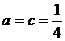 .
.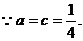
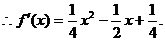
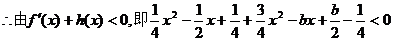
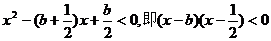
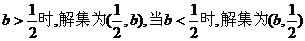 ,当
,当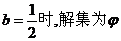 .
.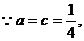
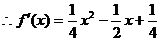
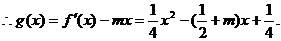
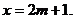
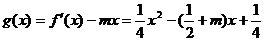 区间
区间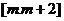 上有
上有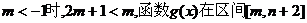 上是递增的.
上是递增的.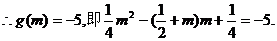
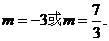
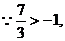
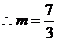 舍去
舍去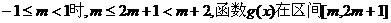 上是递减的,而在
上是递减的,而在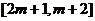 上是递增的,
上是递增的,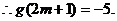
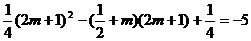
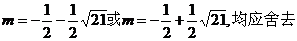
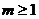 时,
时,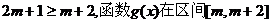 上递减的
上递减的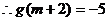
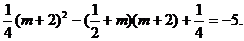
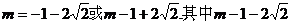 应舍去.
应舍去. 时,
时,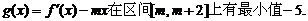
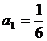 ,前n项和
,前n项和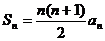 ,
,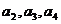
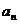 ,并用数学归纳法证明。
,并用数学归纳法证明。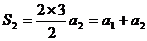 得:
得: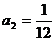
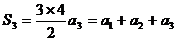 得:
得: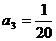
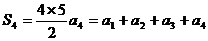 得:
得: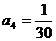
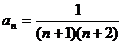
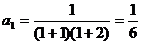 ,等式成立。
,等式成立。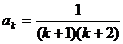 ,当n=k+1时,
,当n=k+1时,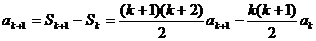
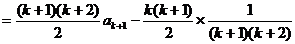
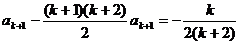
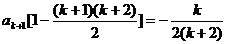
 ,综合①②,等式成立。
,综合①②,等式成立。 在三棱锥
在三棱锥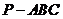 中,
中,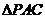 和
和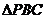 是边长为
是边长为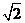 的等边三角形,
的等边三角形,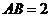 ,
,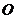 是
是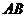 中点.
中点.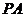 上求一点
上求一点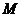 ,使得
,使得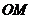 ∥平面
∥平面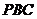 ;
; 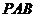 ⊥平面
⊥平面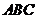 ;
;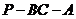 的余弦值.
的余弦值.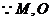 分别为
分别为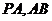 中点,
中点,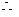

 平面
平面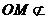 平面
平面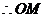 ∥平面
∥平面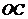 ,
,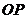
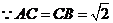 ,
, ⊥
⊥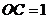 .
.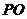 ⊥
⊥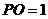 .
. 又
又 ,
,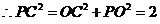 ,
,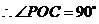 .
.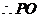 ⊥
⊥
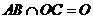 ,
,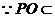 平面
平面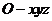 .
.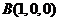 ,
,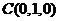 ,
,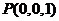 ,
, 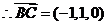 ,
,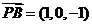 .
.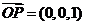 是平面
是平面 ,
,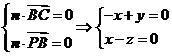 .
. ,则
,则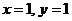 ,
,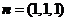 .
. .
.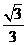 .
.