
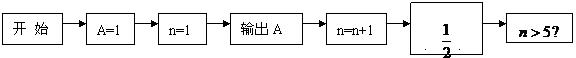 探究1:根据图中框图,写出所打印数列的前5项,并建立数列的递推公式,这个数列是等比数列吗?
探究1:根据图中框图,写出所打印数列的前5项,并建立数列的递推公式,这个数列是等比数列吗?

解:若将打印出来的数依次记为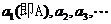 ,由图可知,
,由图可知,



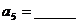
于是可得递推公式
探究2:一个等比数列的第3项和第4项分别是12和18,求它的第1项和第2项;
解:设________________________________________
由已知得
探究3:已知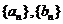 是项数相同的等比数列,仿照下表中的例子填写表格,从中你能得出什么结论?证明你的结论;
是项数相同的等比数列,仿照下表中的例子填写表格,从中你能得出什么结论?证明你的结论;
|
|
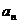 |
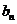 |
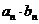 |
判断数列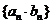 是否等比数列 是否等比数列 |
|
例 |
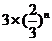 |
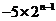 |
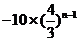 |
是 |
|
自选1 |
|
|
|
|
|
自选2 |
|
|
|
|
解:填表请同学们自己完成;
根据这个表格,我们可以得到:________________________________
证明如下:
变式训练1:如果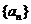 是等比数列,c是不等于0的常数,那么数列
是等比数列,c是不等于0的常数,那么数列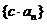 是等比数列吗?并证明你的结论;
是等比数列吗?并证明你的结论;
变式训练2:对于探究3中的等比数列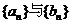 ,数列
,数列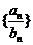 也一定是等比数列吗?并证明你的结论;
也一定是等比数列吗?并证明你的结论;
课内练习:当数列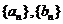 是项数相同的两个等差数列时,数列
是项数相同的两个等差数列时,数列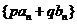 (其中
(其中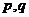 是常数)也是等差数列吗?并证明你的结论;
是常数)也是等差数列吗?并证明你的结论;
课后活动:
1等比数列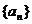 的各项均为正数,且
的各项均为正数,且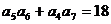 则
则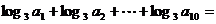 ( )
( )
A、12
B、10 C、8
D、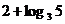
2、已知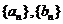 都是等比数列,那么( )
都是等比数列,那么( )
A、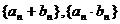 都一定是等比数列 B、
都一定是等比数列 B、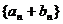 一定是等比数列,但
一定是等比数列,但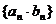 不一定是等比数列 C、
不一定是等比数列 C、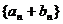 不一定是等比数列,但
不一定是等比数列,但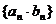 一定是等比数列 D、
一定是等比数列 D、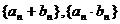 都不一定是等比数列
都不一定是等比数列
1、等差数列与等比数列对照表:
|
名称 |
等差数列 |
等比数列 |
|
定义式 |
|
|
|
通项公式 |
|
|
|
中项公式 |
|
|
|
性质1 |
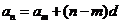 |
|
|
性质2 |
 |
|
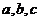 成等比数列,则函数
成等比数列,则函数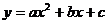 的图象与
的图象与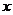 轴交点个数是
轴交点个数是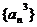 ;②
;②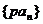 (
(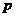 是非零常数);③
是非零常数);③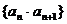 ;④
;④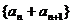 ,其中等比数列的个数为( )
,其中等比数列的个数为( ) )(ω>0)的单调区间,只需求y=Asin(ωx+
)(ω>0)的单调区间,只需求y=Asin(ωx+