16、(12分)已知 ,设命题
,设命题 函数
函数 在
在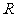 上单调递增,命题
上单调递增,命题 不等式
不等式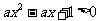 对
对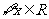 恒成立。若“
恒成立。若“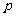 且
且 ”为假,“
”为假,“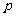 或
或 ”为真,求
”为真,求 的取值范围。
的取值范围。
解:由函数 在
在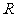 上单调递增,可得
上单调递增,可得
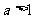
再由不等式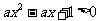 对
对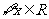 恒成立,可得
恒成立,可得


由于“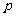 且
且 ”为假,“
”为假,“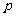 或
或 ”为真,故有
”为真,故有
 或
或


16、(12分)已知 ,设命题
,设命题 函数
函数 在
在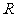 上单调递增,命题
上单调递增,命题 不等式
不等式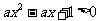 对
对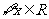 恒成立。若“
恒成立。若“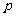 且
且 ”为假,“
”为假,“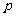 或
或 ”为真,求
”为真,求 的取值范围。
的取值范围。
解:由函数 在
在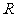 上单调递增,可得
上单调递增,可得
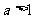
再由不等式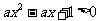 对
对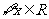 恒成立,可得
恒成立,可得


由于“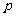 且
且 ”为假,“
”为假,“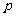 或
或 ”为真,故有
”为真,故有
 或
或

