摘要:已知函数图象上一点处的切线方程为 . (Ⅰ)求的值, (Ⅱ)若方程在内有两个不等实根.求的取值范围(其中为自然对数的底数.), (Ⅲ)令.如果图象与轴交于,().中点为.求证:在处的导数. 解:(Ⅰ)... ∴.且. -------- 2分 解得. -------- 3分 (Ⅱ).令. 则.令.得(舍去). 在内.当时.. ∴ 是增函数, 当时.. ∴ 是减函数 -------- 5分 则方程在内有两个不等实根的充要条件是----7分 即. ----------- 8分 (Ⅲ).. 假设结论成立.则有 ---------- 9分 ①-②.得. ∴. -------------------- 10分 由④得. ∴.即. 即.⑤ -------------------- 11分 令.(). -------------- 12分 则>0.∴在上增函数. ∴. --- 14分 ∴⑤式不成立.与假设矛盾.
网址:http://m.1010jiajiao.com/timu_id_4418417[举报]
已知函数![]() 图象上一点
图象上一点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若方程![]() 在
在![]() 内有两个不等实根,求
内有两个不等实根,求![]() 的取值范围(其中
的取值范围(其中![]() 为自然对数的底数);
为自然对数的底数);
(Ⅲ)令![]() ,若
,若![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() (其中
(其中![]() ),
),![]() 的中点为
的中点为![]() ,求证:
,求证:![]() 在
在![]() 处的导数
处的导数![]() .
.
已知函数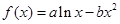 图象上一点
图象上一点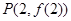 处的切线方程为
处的切线方程为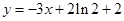 .
.
(1)求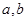 的值;
的值;
(2)若方程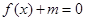 在
在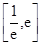 内有两个不等实根,求
内有两个不等实根,求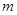 的取值范围(其中
的取值范围(其中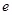 为自然对数的底数);(3)令
为自然对数的底数);(3)令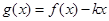 ,若
,若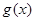 的图象与
的图象与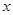 轴交于
轴交于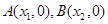 (其中
(其中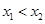 ),
),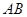 的中点为
的中点为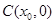 ,求证:
,求证: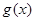 在
在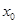 处的导数
处的导数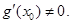
查看习题详情和答案>>
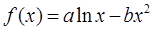 图象上一点
图象上一点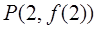 处
处 在
在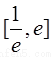 内有两个不等实根,求m的取值范围(其
内有两个不等实根,求m的取值范围(其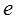 为自然对数的底数);
为自然对数的底数);  图象上一点
图象上一点 处的切线方程为
处的切线方程为 .
. 的值;
的值; 在
在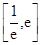 内有两个不等实根,求
内有两个不等实根,求 的取值范围(其中
的取值范围(其中 为自然对数的底数);(3)令
为自然对数的底数);(3)令 ,若
,若 的图象与
的图象与 轴交于
轴交于 (其中
(其中 ),
), 的中点为
的中点为 ,求证:
,求证: 处的导数
处的导数
 图象上一点
图象上一点 处
处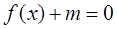 在
在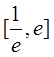 内有两个不等实根,求m的取值范围(其
内有两个不等实根,求m的取值范围(其 为自然对数的底数);
为自然对数的底数);