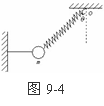
[例1](★★★★)如图9-4 ,轻弹簧和一根细线共同拉住一质量为m的物体,平衡时细线水平,弹簧与竖直夹角为θ ,若突然剪断细线,刚刚剪断细线的瞬间,物体的加速度多大?
 命题意图:考查理解能力及推理判断能力。B级要求。
命题意图:考查理解能力及推理判断能力。B级要求。
错解分析:对弹簧模型与绳模型瞬态变化的特征不能加以区分,误认为“弹簧弹力在细线剪断的瞬间发生突变”从而导致错解。
解题方法与技巧:
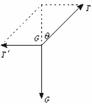 弹簧剪断前分析受力如图9-5 ,由几何关系可知:
弹簧剪断前分析受力如图9-5 ,由几何关系可知:
|
图9-5 |
弹簧的弹力T = mg/cosθ
细线的弹力T′ = mgtanθ
 细线剪断后由于弹簧的弹力及重力均不变,故物体的合力水平向右,与T′等大而反向,ΣF = mgtanθ ,故物体的加速度a = gtanθ ,水平向右。
细线剪断后由于弹簧的弹力及重力均不变,故物体的合力水平向右,与T′等大而反向,ΣF = mgtanθ ,故物体的加速度a = gtanθ ,水平向右。
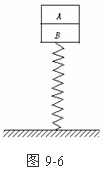
[例2](★★★★★)A、B两木块叠放在竖直轻弹簧上,如图9-6所示,已知木块A 、B质量分别为0.42kg和0.40kg ,弹簧的劲度系数k = 100N/m ,若在木块A上作用一个竖直向上的力F ,使A由静止开始以0.5m/s2的加速度竖直向上做匀加速运动(g = 10m/s2)。
(1)使木块A竖直做匀加速运动的过程中,力F的最大值;
(2)若木块由静止开始做匀加速运动,直到A 、B分离的过程中,弹簧的弹性势能减少了0.248J ,求这一过程F对木块做的功。
命题意图:考查对物理过程、状态的综合分析能力。B级要求。
错解分析:此题难点和失分点在于能否通过对此物理过程的分析后,确定两物体分离的临界点,即当弹簧作用下的两物体加速度、速度相同且相互作用的弹力 N = 0时 ,恰好分离。
解题方法与技巧:
当F = 0(即不加竖直向上F力时),设A 、B叠放在弹簧上处于平衡时弹簧的压缩量为x ,有:
 kx =(mA + mB)g
kx =(mA + mB)g
x =(mA + mB)g/k ①
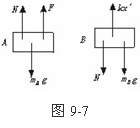
对A施加F力,分析A、B受力如图9-7
对A F + N-mAg = mAa ②
对B kx′-N-mBg = mBa′ ③
可知,当N≠0时,AB有共同加速度a = a′,由②式知欲使A匀加速运动,随N减小F增大。当N = 0时,F取得了最大值Fm ,
即Fm = mA(g + a)= 4.41N
又当N = 0时,A、B开始分离,由③式知,
此时,弹簧压缩量kx′= mB(a + g)
x′= mB(a + g)/k ④
AB共同速度 v2 = 2a(x-x′) ⑤
由题知,此过程弹性势能减少了WP = EP = 0.248J
设F力功WF ,对这一过程应用动能定理或功能原理,有:
WF + EP-(mA+mB)g(x-x′)=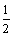 (mA + mB)v2 ⑥
(mA + mB)v2 ⑥
联立①④⑤⑥,且注意到EP = 0.248J
可知,WF = 9.64×10-2J
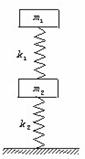
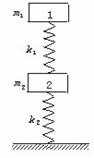
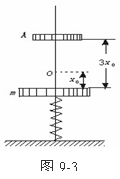 (★★★★)如图9-2所示,劲度系数为k1的轻质弹簧两端分别与质量为m1 、m2的物块1、2拴接,劲度系数为k2的轻质弹簧上端与物块2拴接,下端压在桌面上(不拴接),整个系统处于平衡状态。现施力将物块1缓慢地竖直上提,直到下面那个弹簧的下端刚脱离桌面。在此过程中,物块2的重力势能增加了______,物块1的重力势能增加了________。
(★★★★)如图9-2所示,劲度系数为k1的轻质弹簧两端分别与质量为m1 、m2的物块1、2拴接,劲度系数为k2的轻质弹簧上端与物块2拴接,下端压在桌面上(不拴接),整个系统处于平衡状态。现施力将物块1缓慢地竖直上提,直到下面那个弹簧的下端刚脱离桌面。在此过程中,物块2的重力势能增加了______,物块1的重力势能增加了________。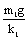 B、
B、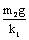 C、
C、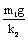 D、
D、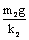
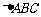 中,已知
中,已知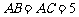 cm,
cm, cm,动点P、Q分别从A、B两点同时出发,沿AB、BC方向匀速移动,它们的速度都是1 cm/秒.
当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(秒).
cm,动点P、Q分别从A、B两点同时出发,沿AB、BC方向匀速移动,它们的速度都是1 cm/秒.
当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(秒).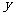 cm2,写出
cm2,写出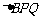 与
与
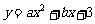 与
与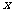 轴交于A、B两点,
轴交于A、B两点,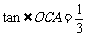 ,
,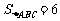 .
.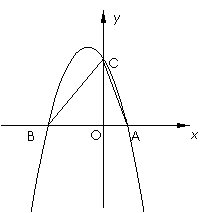 (3)设点E在
(3)设点E在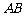 ∥
∥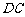 ,
, ,
,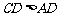 ,将纸片沿过点D的直线折叠,使点A落在边CD上的点E处,折痕为
,将纸片沿过点D的直线折叠,使点A落在边CD上的点E处,折痕为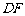 .连接EF并展开纸片.
.连接EF并展开纸片.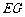 ,如果
,如果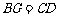 ,试说明四边形GBCE是等腰梯形.
,试说明四边形GBCE是等腰梯形.