摘要: 在等腰中.已知cm.cm.动点P.Q分别从A.B两点同时出发.沿AB.BC方向匀速移动.它们的速度都是1 cm/秒. 当点P到达点B时.P.Q两点停止运动.设点P的运动时间为t(秒). (1)当t为何值时.PQ⊥AB? (2)设四边形APQC的面积为cm2.写出关于t的函数关系式及定义域, (3)分别以P.Q为圆心.PA.BQ长为半径画圆.若⊙P与⊙Q相切.求t的值, (4)在P.Q运动中.与能否相似?若能.请求出AP的长,若不能.请说明理由. 崇明县2009年初三学业考试模拟考
网址:http://m.1010jiajiao.com/timu_id_4406913[举报]
(本题满分14分,其中第(1)题4分,第(2)题的第?、?小题分别为4分、6分)
如图1,在△ABC中,已知AB=15,cosB=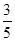 ,tanC=
,tanC=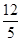 .点D为边BC上的动点(点D不与B、C重合),以D为圆心,BD为半径的⊙D交边AB于点E.
.点D为边BC上的动点(点D不与B、C重合),以D为圆心,BD为半径的⊙D交边AB于点E.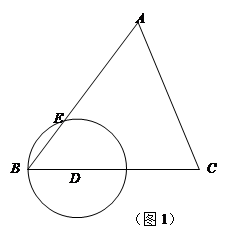
(1)设BD=x,AE=y,求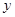 与
与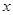 的函数关系式,并写出函数定域义;
的函数关系式,并写出函数定域义;
(2)如图2,点F为边AC上的动点,且满足BD=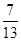 CF,联结DF.
CF,联结DF.
①当△ABC和△FDC相似时,求⊙D的半径;
② 当⊙D与以点F为圆心,FC为半径⊙F外切时,求⊙D的半径.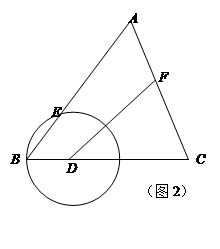
(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)在Rt△ABC中,∠ACB=90°,BC=30,AB=50.点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于E.点M在线段AP上,点N在线段BP上,EM=EN,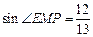 .
.
(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A、C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出函数的定义域;
(3)若△AME∽△ENB(△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应),求AP的长.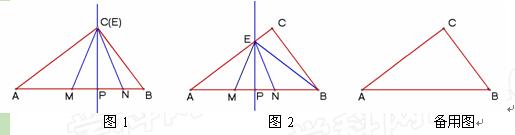 查看习题详情和答案>>
查看习题详情和答案>>
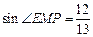 .
.(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A、C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出函数的定义域;
(3)若△AME∽△ENB(△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应),求AP的长.
 查看习题详情和答案>>
查看习题详情和答案>>
(本题满分14分)
如图,在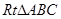 中,
中,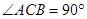 ,
, 是斜边
是斜边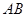 上的中线,
上的中线,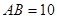 ,
,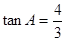 ,点
,点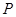 是
是 延长线上的一动点,过点
延长线上的一动点,过点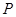 作
作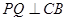 ,交
,交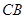 延长线于点
延长线于点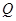 ,
,
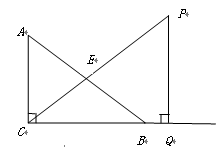
设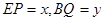 .
.
【小题1】(1)求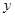 关于
关于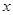 的函数关系式及定义域;(4分)
的函数关系式及定义域;(4分)
【小题2】(2)联结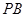 ,当
,当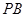 平分
平分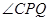 时,求
时,求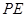 的长;(4分)
的长;(4分)
【小题3】(3)过点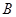 作
作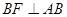 交
交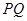 于
于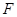 ,当
,当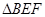 和
和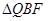 相似时,求
相似时,求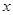
 的值.(6分)
的值.(6分)

 与x轴交于A、B两点,与y轴交于C点,点P从A
与x轴交于A、B两点,与y轴交于C点,点P从A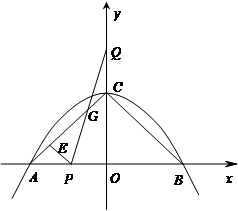 点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。