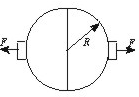
1.(★★★)两个半球壳折成的球形容器内部已抽成真空,球形容器的半径为R ,大气压强为p 。为使两个半球壳沿图26-5中箭头方向互相分离,应施加的力F至少为:
 |
|
图26-5 |
A、4πR2p B、2πR2p
C、πR2p D、 πR2p
πR2p
 |
|
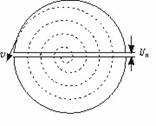
图26-2 |
[例1](★★★★)(物理过程的等效)如图26-2所示,已知回旋加速器中,D形盒内匀强磁场的磁感应强度B = 1.5T ,盒的半径R = 60cm ,两盒间隙d = 1.0cm ,盒间电压U = 2.0×104V ,今将α粒子从近于间隙中心某点向D形盒内以近似于零的初速度垂直B的方向射入,求粒子在加速器内运行的总时间。
命题意图:考查综合分析及推理能力。B级要求。
错解分析:考生对α粒子运动过程缺乏分解和总体把握,不能运用等效办法求解在电场中加速的时间,陷入逐段分析求和的泥潭,导致错解。
解题方法与技巧:带电粒子在回旋加速器转第一周,经两次加速,速度为v1 ,则根据动能定理得:2qU = m
m
设运转n周后,速度为v ,则:
n2qU
= mv2
①
mv2
①
由牛顿第二定律,qvB = m ②
②
由①②得粒子转动n = 周。
周。
粒子在加速器内运行的总时间t = tB + tE ,
在磁场中运动每周等时,则在磁场中的总时间:
tB = nT = n
 =
=

 =
=
而在间隙处电场中运动时间为tE ,因每次时间不等(且次数又多,分段算将十分繁琐),我们可将各段间隙等效“衔接”起来,展开成一准直线,则粒子在电场中运动就可视作初速度为零的匀加速直线运动,由公式:tE = ,且v0 = 0 ,vt =
,且v0 = 0 ,vt = ,a =
,a = 得:
得:
tE =
故:t = tB + tE = (
( + d) =
4.5×10-5×(0.94 + 0.01)= 4.3×10-5s 。
+ d) =
4.5×10-5×(0.94 + 0.01)= 4.3×10-5s 。
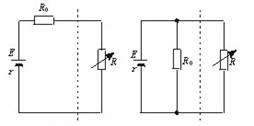 [例2](★★★★)(物理模型的变换等效)如图26-3所示的甲、乙两个电路中电源电动势E和内电阻r已知,定值电阻R已知,求电阻R调至多大时,R上获得的电功率最大,其最大值为多少?电源在什么条件下输出功率最大?
[例2](★★★★)(物理模型的变换等效)如图26-3所示的甲、乙两个电路中电源电动势E和内电阻r已知,定值电阻R已知,求电阻R调至多大时,R上获得的电功率最大,其最大值为多少?电源在什么条件下输出功率最大?
命题意图:考查综合分析能力及运用已学知识灵活解决物理问题的能力。B级要求。
|
图26-3 |
错解分析:考生往往借助常规思路,据闭合电路欧姆定律及直流电路特点,写出R的功率表达式,讨论求解,繁杂易错,思维缺乏灵活性。
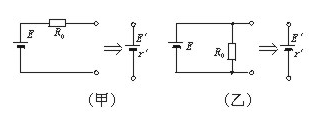
解题方法与技巧:本题用隔离法分析比较巧妙,设沿虚线将电路隔离成左、右两部分,左边部分可以看作一个新的电源,对(甲)图电路来说,新电源的电动势为E′= E ,而内电阻r′= r + R0 ,对(乙)图来说,新电源的电动势为E′= E ,而r′=
E ,而r′= ,如图26-4所示。虚线右边部分即为新电源的外电阻R。这种新电源又叫做等效电源。
,如图26-4所示。虚线右边部分即为新电源的外电阻R。这种新电源又叫做等效电源。
 |
|
图26-4 |
这样原来的甲乙电路就简化成了由等效电源(E′,r′)与电阻R连成的最简单电路。由电源的输出功率(即外电路上R获得的电功率)与外电阻R的关系知,在(甲)图中当R = r′= r + R0时,R上获得的电功率最大,其最大功率为Pm = =
= 。对(乙)图中当R = r′=
。对(乙)图中当R = r′= 时R上获得的功率最大,最大功率为:
时R上获得的功率最大,最大功率为:
Pm = =
= =
=
25.(本题满分14分,第(1)小题满分6分,第(2)小题满分5分,第(3)小题满分3分)
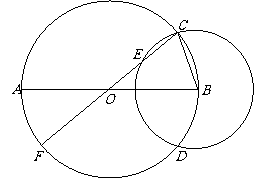 已知:⊙O的直径AB=8,⊙B与⊙O相交于点C、D,⊙O的直径CF与⊙B相交于点E,设⊙B的半径为
已知:⊙O的直径AB=8,⊙B与⊙O相交于点C、D,⊙O的直径CF与⊙B相交于点E,设⊙B的半径为 ,OE的长为
,OE的长为 ,
,
(1) 如图7,当点E在线段OC上时,求 关于
关于 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(2) 当点E在直径CF上时,如果OE的长为3,求公共弦CD的长;
(3) 
|
 )T/s ,求L1的功率。
)T/s ,求L1的功率。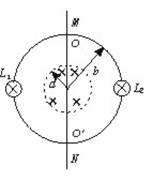
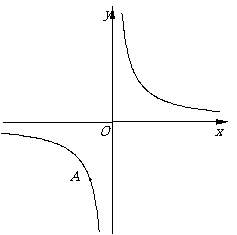 已知:如图6,点A(–2,–6)在反比例函数的图像上,如果点B也在此反比例函数图像上,直线AB与 y轴相交于点C,且BC=2AC .
已知:如图6,点A(–2,–6)在反比例函数的图像上,如果点B也在此反比例函数图像上,直线AB与 y轴相交于点C,且BC=2AC . 的图像经过A、B两点,求此二次函数的解析式.
的图像经过A、B两点,求此二次函数的解析式. (本题满分12分)
(本题满分12分) .
.