摘要：例5．(2003年普通高等学校招生全国统一考试 在某海滨城市附近海面有一台风.据监测.当前台风中心位于城市O的东偏南方向300km的海面P处.并以20km/h的速度向西偏北45°方向移动. 台风侵袭的范围为圆形区域.当前半径为60km.并以10km/h的速度不断增大. 问几小时后该城市开始受到台风的侵袭?解:如图建立坐标系以O为原点.正东方向为x轴正向. 在时刻:的坐标为此时台风侵袭的区域是其中若在t时刻城市O受到台风的侵袭.则有 即答:12小时后该城市开始受到台风的侵袭.
网址：http://m.1010jiajiao.com/timu_id_78198[举报]
例10．（2004年重庆卷）某工厂生产某种产品，已知该产品的月生产量（吨）与每吨产品的价格（元/吨）之间的关系式为：,且生产x吨的成本为（元）.问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入─成本）
解：每月生产x吨时的利润为
，故它就是最大值点，且最大值为：
答：每月生产200吨产品时利润达到最大，最大利润为315万元.
据权威人士分析“严格来讲，我国目前已进入负利率时代”，“钱在银行缩水”．以一年期存款利率1．98%为例，现考虑2003年物价指数上升3．2%和利息税20%两方面因素，实际利息率为-1．616%（即1．98%×(1-20%)-3．2%），这意味将100000元人民币存入银行，1年后实际价值为98384元，1616元白白“蒸发”．据初步估计2004年物价指数将上升2．2%，假设其它条件不变，请你计算一下某人2004年年初存入银行100000元，1年后的实际价值变为
- A.99464元
- B.99384元
- C.98384元
- D.100616元
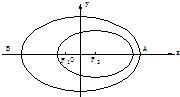2003年10月15日9时，“神舟”五号载人飞船发射升空，于9时9分50秒准确进入预定轨道，开始巡天飞行．该轨道是以地球的中心F2为一个焦点的椭圆．选取坐标系如图所示，椭圆中心在原点．近地点A距地面200km，远地点B距地面350km．已知地球半径R=6371km．（I）求飞船飞行的椭圆轨道的方程；
（II）飞船绕地球飞行了十四圈后，于16日5时59分返
回舱与推进舱分离，结束巡天飞行，飞船共巡天飞行了约6×105km，问飞船巡天飞行的平均速度是多少km/s？
（结果精确到1km/s）（注：km/s即千米/秒） 查看习题详情和答案>>
某企业常年生产一种出口产品，根据需求预测：进入21世纪以来，前8年在正常情况下，该产品产量将平衡增长．已知2000年为第一年，头4年年产量f（x）（万件）如表所示：
（1）建系，画出2000～2003年该企业年产量的散点图；
（2）建立一个能基本反映（误差小于0.1）这一时期该企业年产量发展变化的函数模型，并求之．
（3）2013年（即x=14）因受到某外国对我国该产品反倾销的影响，年产量应减少30%，试根据所建立的函数模型，确定2013年的年产量应该约为多少？
查看习题详情和答案>>
| x | 1 | 2 | 3 | 4 |
| f（x） | 4.00 | 5.58 | 7.00 | 8.44 |
（2）建立一个能基本反映（误差小于0.1）这一时期该企业年产量发展变化的函数模型，并求之．
（3）2013年（即x=14）因受到某外国对我国该产品反倾销的影响，年产量应减少30%，试根据所建立的函数模型，确定2013年的年产量应该约为多少？
从1999年到2002年期间，甲每年6月1日都到银行存入m元一年定期储蓄，若年利率q保持不变，且每年到期的存款利息均自动转为新的一年定期，到2003年6月1日，甲去银行不再存款，而是将所有存款的本息作用全部取回，则取回的金额是（ ）
| A、m（1+q）4元 | ||
B、
| ||
| C、m（1+q）5元 | ||
D、
|