Question

某企业常年生产一种出口产品，根据需求预测：进入21世纪以来，前8年在正常情况下，该产品产量将平衡增长．已知2000年为第一年，头4年年产量f（x）（万件）如表所示：

x	1	2	3	4
f（x）	4.00	5.58	7.00	8.44

（1）建系，画出2000～2003年该企业年产量的散点图；
（2）建立一个能基本反映（误差小于0.1）这一时期该企业年产量发展变化的函数模型，并求之．
（3）2013年（即x=14）因受到某外国对我国该产品反倾销的影响，年产量应减少30%，试根据所建立的函数模型，确定2013年的年产量应该约为多少？

Answer 1

分析：（1）直接由表格画出散点图；
（2）由散点图看出函数模型近似为一次函数模型，代入已知两个点的坐标，求出函数解析式，验证后说明函数模型的可行性；
（3）把x=14代入模型求出f（14）的值，乘以70%后得答案．

解答：解：（1）散点图如图：

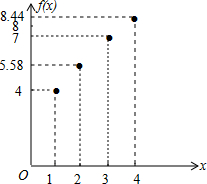
（2）设f（x）=ax+b，把点（1，4），（3，7）代入直线模型得：

a+b=4 3a+b=7

，解得

a= 3 2 b= 5 2

．
∴f(x)=

3

2

x+

5

2

．
检验：f（2）=5.5，|5.58-5.5|=0.08＜0.1；
f（4）=8.5，|8.44-8.5|=0.06＜0.1．
∴模型f(x)=

3

2

x+

5

2

能基本反映产量变化；
（3）f（14）=

3

2

×14+

5

2

=23.5，
由题意知，2013年的年产量约为23.5×70%=16.45（万件），即2013年的年产量应约为16.45万件．

点评：本题考查了函数模型的选择及应用，考查了回归分析的基本思想及初步应用，是中档题．