摘要：适当将一些常规性题目改造为开放型题如可以把条件.结论完整的题目改造成给出条件.先猜结论.再进行证明的形式,也可以改造给出多个条件.需要整理.筛选以后才能求解或证明的题目,还可以改造成要求运用多种解法或得出多个结论的题目.以加强发散式思维的训练.此外.将题目的条件.结论拓广.使其演变为一个发展性问题.或给出结论.再让学生探求条件等.都是使常规性题目变为开放题的有效方法.例如:高中教材中有这样一个例题:平面内条直线.任何两条不平行.任何三条不过同一点.证明:这条直线的交点的个数为.对此问题可以把它改造为:某地区有条直线型铁路线.在每条铁路线的交点处设一车站.至多设多少个车站?通过这样的改造.常规性题目便具备了开放题的形式.例题的功能也得以更充分的发挥.当然此题还可以进一步变换条件.引申推广.
网址：http://m.1010jiajiao.com/timu_id_7623[举报]
某地位于沙漠边缘地区，人与自然进行长期顽强的斗争，到2001年底全地区的绿化率已达到30%，从2002年开始，每年将出现下列变化：原沙漠面积的16%将栽上树改造为绿洲，原有绿洲面积的4%又被侵蚀，变为沙漠，
（1）设全地区面积为1，2001年底绿洲面积为a1=
，经过一年绿洲面积为a2，经过n年绿洲面积为an+1，写出an与an+1的关系式并求证数列{an-
}是等比数列；
（2）问经过努力到哪一年才能使全县的绿洲面积超过60%．
查看习题详情和答案>>
（1）设全地区面积为1，2001年底绿洲面积为a1=
| 3 |
| 10 |
| 4 |
| 5 |
（2）问经过努力到哪一年才能使全县的绿洲面积超过60%．
（本题满分13分）
一个截面为抛物线形的旧河道(如图1)，河口宽
米，河深2米，现要将其截面改造为等腰梯形(如图2)，要求河道深度不变，而且施工时只能挖土，不准向河道填土．
(Ⅰ)建立恰当的直角坐标系并求出抛物线弧
的标准方程；
(Ⅱ)试求当截面梯形的下底（较长的底边）长为多少米时，才能使挖出的土最少？
有一长为10m的斜坡，它的倾斜角是75°，在不改变坡高和坡顶的前提下，通过加长坡面的方法将它的倾斜角改为30°（如图）.则坡底要延伸 （ ）
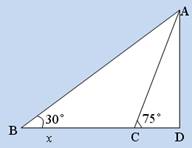
A、5m B、10m C、10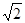
m D、10
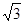m
查看习题详情和答案>>
小明家中有两种酒杯,一种酒杯的轴截面是等腰直角三角形,称之为直角酒杯,另一种酒杯的轴截面近似一条抛物线,杯口宽4 cm,杯深为8 cm,称之为抛物线酒杯.
(1)请选择适当的坐标系,求出抛物线酒杯的方程.
(2)一次,小明在游戏中注意到一个现象,若将一些大小不等的玻璃球依次放入直角酒杯中,则任何玻璃球都不能触及酒杯杯底.但若将这些玻璃球放入抛物线酒杯中,则有些小玻璃球能触及酒杯杯底.小明想用所学数学知识研究一下,当玻璃球的半径r为多大值时,玻璃球一定会触及酒杯杯底.你能帮助小明解决这个问题吗?
(3)在抛物线酒杯中,放入一根粗细均匀、长度为2 cm的细棒,假设细棒的端点与酒杯壁之间的摩擦可以忽略不计,那么当细棒最后达到平衡状态时,细棒在酒杯中位置如何?
