题目内容
某地区气候条件恶劣,且位于沙漠边缘地带,到2011年底该地区的绿化率只有30%,计划从2012年开始加大沙漠化改造的力度,每年将原来沙漠面积的16%改造为绿洲,但同时原有绿洲面积的4%还会被沙漠化.
(1)设该地区的总面积为a,2011年底的绿洲面积为a1=
a,经过一年治理后绿洲面积为a2,…,经过n年后绿洲面积为an+1,求证:an+1=
an+
;
(2)问至少需要经过多少的努力,才能使该地区的绿洲面积超过60%?(参考数据:lg2=0.3)
(1)设该地区的总面积为a,2011年底的绿洲面积为a1=
| 3 |
| 10 |
| 4 |
| 5 |
| 4 |
| 25 |
(2)问至少需要经过多少的努力,才能使该地区的绿洲面积超过60%?(参考数据:lg2=0.3)
分析:(1)经过n年后绿洲面积由两部分组成,一部分是原有的绿洲面积减去沙漠化后剩下的面积为96%an,另一部分是新绿洲化的面积16%bn,由此可得结论;
(2)先确定an+1=
a-
a×(
)n,再建立不等式,即可得到结论.
(2)先确定an+1=
| 4 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
解答:(1)证明:设2011年底沙漠面积为b1,经过n年沙漠面积为bn+1,则a1+b1=a,
依题意,an+1由两部分组成,一部分是原有的绿洲面积减去沙漠化后剩下的面积为96%an,另一部分是新绿洲化的面积16%bn,
∴an+1=96%an+16%bn=
an+
a;
(2)解:由(1)可知an+1-
a=
(an-
a)
∴{an-
a}是以-
a为首项,
为公比的等比数列
∴an+1=
a-
a×(
)n
依题意:
a-
a×(
)n>60%a
∴(
)n<
∴n>
=
=4
∴至少需要5年才能达到目标.
依题意,an+1由两部分组成,一部分是原有的绿洲面积减去沙漠化后剩下的面积为96%an,另一部分是新绿洲化的面积16%bn,
∴an+1=96%an+16%bn=
| 4 |
| 5 |
| 4 |
| 25 |
(2)解:由(1)可知an+1-
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
∴{an-
| 4 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
∴an+1=
| 4 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
依题意:
| 4 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
∴(
| 4 |
| 5 |
| 2 |
| 5 |
∴n>
lg
| ||
lg
|
| 1-2lg2 |
| 1-3lg2 |
∴至少需要5年才能达到目标.
点评:本题考查数列模型的构建,考查数列通项的求解,考查解不等式,属于中档题.

练习册系列答案
相关题目
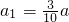 ,经过一年治理后绿洲面积为a2,…,经过n年后绿洲面积为an+1,求证:
,经过一年治理后绿洲面积为a2,…,经过n年后绿洲面积为an+1,求证: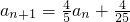 ;
;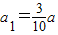 ,经过一年治理后绿洲面积为a2,…,经过n年后绿洲面积为an+1,求证:
,经过一年治理后绿洲面积为a2,…,经过n年后绿洲面积为an+1,求证: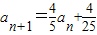 ;
;