题目内容
(本题满分13分)
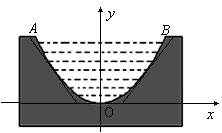
一个截面为抛物线形的旧河道(如图1),河口宽![]() 米,河深2米,现要将其截面改造为等腰梯形(如图2),要求河道深度不变,而且施工时只能挖土,不准向河道填土.
米,河深2米,现要将其截面改造为等腰梯形(如图2),要求河道深度不变,而且施工时只能挖土,不准向河道填土.
(Ⅰ)建立恰当的直角坐标系并求出抛物线弧![]() 的标准方程;
的标准方程;
(Ⅱ)试求当截面梯形的下底(较长的底边)长为多少米时,才能使挖出的土最少?

解:(1)如图:以抛物线的顶点为原点,
![]() 中垂线为
中垂线为![]() 轴建立直角坐标系------1分
轴建立直角坐标系------1分
 则
则![]() ------2分
------2分
设抛物线的方程为![]() ,将点
,将点![]() 代入得
代入得![]() -------3分
-------3分
所以抛物线弧AB方程为![]() (
(![]() ) ------4分
) ------4分
(2)解法一:
设等腰梯形的腰与抛物线相切于![]()
![]()
则过![]() 的切线
的切线![]() 的斜率为
的斜率为![]()
所以切线![]() 的方程为:
的方程为:![]() ,即
,即![]()
令![]() ,得
,得![]() , 令
, 令![]() ,得
,得![]() ,
,
所以梯形面积![]() -----10分
-----10分
当仅当![]() ,即
,即![]() 时,
时,![]() 成立
成立
此时下底边长为![]() -----12分
-----12分
答:当梯形的下底边长等于![]() 米时,挖出的土最少. -----13分
米时,挖出的土最少. -----13分
解法二:设等腰梯形的腰与抛物线相切于![]()
![]()
则过![]() 的切线
的切线![]() 的斜率为
的斜率为![]()
所以切线![]() 的方程为:
的方程为:![]() ,即
,即![]()
运用定积分计算抛物线与等腰梯形间的面积:
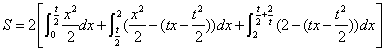 -----10分
-----10分
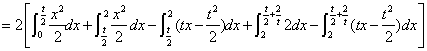
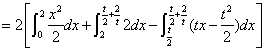
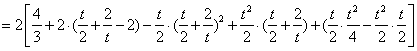
![]()
![]()
当仅当![]() ,即
,即![]() 时,
时,![]() 成立,此时下底边长为
成立,此时下底边长为![]() ---12分
---12分
答:当梯形的下底边长等于![]() 米时,挖出的土最少. -----------13分
米时,挖出的土最少. -----------13分
解法三:设等腰梯形上底(较短的边)长为![]() 米,则一腰过点
米,则一腰过点![]() ,可设此腰所在直线方程为
,可设此腰所在直线方程为![]() , 联立
, 联立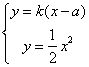 ,得
,得![]() ,
,
令![]() ,得
,得![]() ,或
,或![]() (舍),
(舍),
故此腰所在直线方程为![]() ,
,
令![]() ,得
,得![]() ,
,
故等腰梯形的面积:![]() ------------10分
------------10分
当且仅当![]() ,即
,即![]() 时,有
时,有![]()
此时,下底边长![]() ------------12分
------------12分
答:当梯形的下底边长等于![]() 米时,挖出的土最少. ----------13分
米时,挖出的土最少. ----------13分

 习题精选系列答案
习题精选系列答案 ,
, ,
, .
.  ,
, ; (2) 若
; (2) 若 ,求
,求 的取值范围.
的取值范围. 的三个内角
的三个内角 依次成等差数列.
依次成等差数列. ,试判断
,试判断 ,求
,求
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值. 展开式中,求:
展开式中,求: 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD.
AD. ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.