摘要：6．如下图.有一张直角三角形纸片.两直角边AC=4.BC=8.将△ABC折叠.点B与点A重合.折痕为DE.则CD的长为．
网址：http://m.1010jiajiao.com/timu_id_744827[举报]
小宇手里有一张直角三角形纸片ABC，他无意中将直角边AC折叠了一下，恰好使AC落在斜边AB上，且C点与E点重合，（如图）小宇经过测量得知两直角边AC=6cm，BC=8cm,他想用所学知识求出CD的长，你能帮他吗？
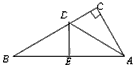
现有一张矩形纸片，只用双手，不借助其他工具，你能将直角三等分吗？
小华是按以下步骤折叠的．
第一步：先把矩形对折，设折痕为MN，如图(1)所示；
第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为H，得Rt△AHE；
第三步：沿EH线折叠，得折痕EF，如图(2)所示，此时，小华说“AE，AH就是∠BAD的三等分线”，你认为对吗？
若对，请证明这个结论；若不对，请说明理由．
将一张矩形纸片沿对角线剪开，得到两张三角形纸片，再将这两张三角形纸片摆放成如下图的形式，使点B、F、C、D在同一条直线上．
（1）求证：AB⊥ED；
（2）若PB=BC，请找出图中与此条件有关的一对全等三角形，并给予证明．
查看习题详情和答案>>
（1）求证：AB⊥ED；
（2）若PB=BC，请找出图中与此条件有关的一对全等三角形，并给予证明．
查看习题详情和答案>>
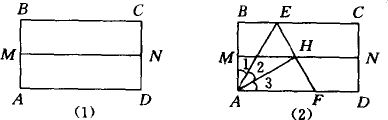
取一张矩形的纸进行折叠，具体操作过程如下：
第一步：先把矩形ABCD对折，折痕为MN，如图（1）所示；
第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B′，得 Rt△AB′E，如图（2）所示；
第三步：沿EB′线折叠得折痕EF，如图（3）所示；利用展开图（4）所示．
探究：
（1）△AEF是什么三角形？证明你的结论．
（2）对于任一矩形，按照上述方法是否都能折出这种三角形？请说明理由．
（3）如图（5），将矩形纸片ABCD沿EF折叠，使点A落在DC边上的点A′处，x轴垂直平分DA，直线EF的表达式为y=kx-k （k＜0）
①问：EF与抛物线y=-
x2 有几个公共点？
②当EF与抛物线只有一个公共点时，设A′（x，y），求
的值．
查看习题详情和答案>>
第一步：先把矩形ABCD对折，折痕为MN，如图（1）所示；
第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B′，得 Rt△AB′E，如图（2）所示；
第三步：沿EB′线折叠得折痕EF，如图（3）所示；利用展开图（4）所示．
探究：
（1）△AEF是什么三角形？证明你的结论．
（2）对于任一矩形，按照上述方法是否都能折出这种三角形？请说明理由．
（3）如图（5），将矩形纸片ABCD沿EF折叠，使点A落在DC边上的点A′处，x轴垂直平分DA，直线EF的表达式为y=kx-k （k＜0）
①问：EF与抛物线y=-
| 1 |
| 8 |
②当EF与抛物线只有一个公共点时，设A′（x，y），求
| x |
| y |
如图①，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在
轴的正半轴上，点C在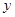
轴的正半轴上，OA=5，OC=4.
（1）在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D、E两点的坐标；
（2）如图②，若AE上有一动点P（不与A、E重合）自A点沿AE方向向E点匀速运动，运动的速度为每秒1个单位长度，设运动的时间为秒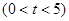
，过P点作ED的平行线交AD于点M，过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间之间的函数关系式；当取何值时，S有最大值？最大值是多少？
（3）在（2）的条件下，当为何值时，以A、M、E为顶点的三角形为等腰三角形，并求出相应时刻点M的坐标.