题目内容
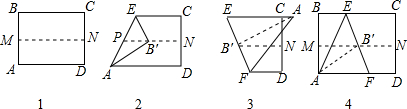
取一张矩形的纸进行折叠,具体操作过程如下:第一步:先把矩形ABCD对折,折痕为MN,如图(1)所示;
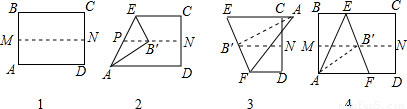
第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B′,得 Rt△AB′E,如图(2)所示;
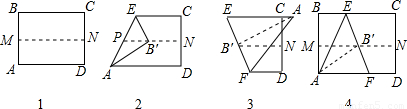
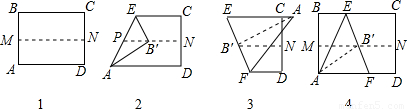
第三步:沿EB′线折叠得折痕EF,如图(3)所示;利用展开图(4)所示.

探究:
(1)△AEF是什么三角形?证明你的结论.
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.
(3)如图(5),将矩形纸片ABCD沿EF折叠,使点A落在DC边上的点A′处,x轴垂直平分DA,直线EF的表达式为y=kx-k (k<0)
①问:EF与抛物线y=-
| 1 |
| 8 |
②当EF与抛物线只有一个公共点时,设A′(x,y),求
| x |
| y |
分析:(1)根据直角三角形斜边上的中线等于斜边的一半,以及矩形性质得出∠AEF=60°,∠EAF=60°,即可得出答案;
(2)根据矩形的长为a,宽为b,可知b≤
a 时,一定能折出等边三角形,当
a<b<a 时,不能折出;
(3)①由已知得出
得到 x2+8kx-8k=0,△=(8k)2+32k=32k(2k+1),再分析k即可得出答案;
②得出Rt△EMO∽Rt△A′AD,进而得出
=
,即可求出答案.
(2)根据矩形的长为a,宽为b,可知b≤
| ||
| 2 |
| ||
| 2 |
(3)①由已知得出
|
②得出Rt△EMO∽Rt△A′AD,进而得出
| OE |
| OM |
| DA/ |
| DA |
解答: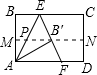 解:(1)△AEF是等边三角形
解:(1)△AEF是等边三角形
证明:∵PE=PA,
B′P是RT△AB′E 斜边上的中线
∴PA=B′P,
∴∠EAB′=∠PB′A,
又∵PN∥AD,
∴∠B′AD=∠PB′A,
又∵2∠EAB′+∠B′AD=90°,
∴∠EAB′=∠B′AD=30°,
易证∠AEF=60°,∴∠EAF=60°,
∴△AEF是等边三角形;
(2)不一定,
设矩形的长为a,宽为b,可知b≤
a 时,一定能折出等边三角形,
当
a<b<a 时,不能折出;
(3)①由
,
得 x2+8kx-8k=0,△=(8k)2+32k=32k(2k+1),
∵k<0.
∴k<-
时,△>0,EF与抛物线有两个公共点.
当k=-
,△=0时,EF与抛物线有一个公共点.
当k>-
,△<0时,EF与抛物线没有公共点,
②EF与抛物线只有一个公共点时,k=-
,
EF的表达式为y=-
x+
,
EF与x轴、y轴的交点为M(1,0),E(0,
),
∵∠EMO=90°-∠OEM=∠EAA′,
∴RT△EMO∽RT△A′AD,
=
,
即
=
,
∴
=1.
 解:(1)△AEF是等边三角形
解:(1)△AEF是等边三角形证明:∵PE=PA,
B′P是RT△AB′E 斜边上的中线
∴PA=B′P,
∴∠EAB′=∠PB′A,
又∵PN∥AD,
∴∠B′AD=∠PB′A,
又∵2∠EAB′+∠B′AD=90°,
∴∠EAB′=∠B′AD=30°,
易证∠AEF=60°,∴∠EAF=60°,
∴△AEF是等边三角形;
(2)不一定,
设矩形的长为a,宽为b,可知b≤
| ||
| 2 |
当
| ||
| 2 |
(3)①由
|
得 x2+8kx-8k=0,△=(8k)2+32k=32k(2k+1),
∵k<0.
∴k<-
| 1 |
| 2 |
当k=-
| 1 |
| 2 |
当k>-
| 1 |
| 2 |
②EF与抛物线只有一个公共点时,k=-
| 1 |
| 2 |
EF的表达式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
EF与x轴、y轴的交点为M(1,0),E(0,
| 1 |
| 2 |
∵∠EMO=90°-∠OEM=∠EAA′,
∴RT△EMO∽RT△A′AD,
| OE |
| OM |
| DA/ |
| DA |
即
| ||
| 1 |
| x |
| 2y |
∴
| x |
| y |
点评:此题主要考查了二次函数的综合应用以及矩形的性质和相似三角形的判定等知识,相似三角形经常与二次函数综合应用,同学们应有意识地运用.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目