题目内容
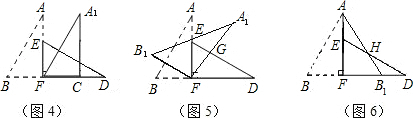
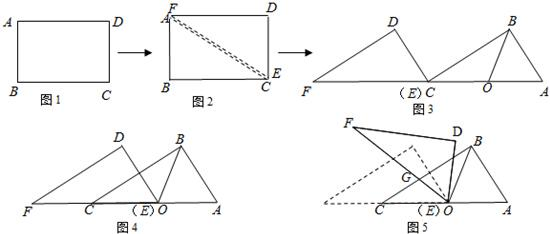
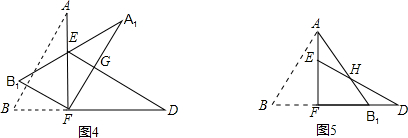
将一张矩形纸片沿对角线剪开,得到两张三角形纸片,再将这两张三角形纸片摆放成如下图的形式,使点B、F、C、D在同一条直线上.(1)求证:AB⊥ED;
(2)若PB=BC,请找出图中与此条件有关的一对全等三角形,并给予证明.

分析:做此题要理解翻折变换后相等的条件,同时利用常用的全等三角形的判定方法来判定其全等.
解答:证明:(1)由题意得,∠A+∠B=90°,∠A=∠D,
∴∠D+∠B=90°,
∴AB⊥DE.(3分)
(2)∵AB⊥DE,AC⊥BD
∴∠BPD=∠ACB=90°,
∴在△ABC和△DBP,
,
∴△ABC≌△DBP(AAS).(8分)
说明:图中与此条件有关的全等三角形还有如下几对:
△APN≌△DCN、△DEF≌△DBP、△EPM≌△BFM.
∴∠D+∠B=90°,
∴AB⊥DE.(3分)
(2)∵AB⊥DE,AC⊥BD
∴∠BPD=∠ACB=90°,
∴在△ABC和△DBP,
|
∴△ABC≌△DBP(AAS).(8分)
说明:图中与此条件有关的全等三角形还有如下几对:
△APN≌△DCN、△DEF≌△DBP、△EPM≌△BFM.
点评:此题考查了翻折变换及全等三角形的判定方法等知识点,常用的判定方法有SSS、SAS、AAS、HL等.

练习册系列答案
相关题目