摘要：7．如下图.以直角坐标系的原点O为圆心.以1为半径作圆.若点P是该圆上第一象限内一点.且OP与轴正方向组成的角为.则P点的坐标为
网址：http://m.1010jiajiao.com/timu_id_737044[举报]
如图，在直角坐标系中，一次函数y=
x+2的图象与x轴交于点A，与y轴交于点B
①若以原点为圆心的圆与直线相切于点C，求C点的坐标；
②在⊙O中剪掉扇形COD后，求剩下的部分做成的圆锥的底面半径（结果用根号表示）．
③在x轴上是否存在这样的点P，使△PAB为等腰三角形？若存在请写出点P坐标；若不存在请说明原因．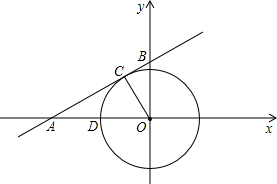
查看习题详情和答案>>
| ||
| 3 |
①若以原点为圆心的圆与直线相切于点C，求C点的坐标；
②在⊙O中剪掉扇形COD后，求剩下的部分做成的圆锥的底面半径（结果用根号表示）．
③在x轴上是否存在这样的点P，使△PAB为等腰三角形？若存在请写出点P坐标；若不存在请说明原因．
查看习题详情和答案>>
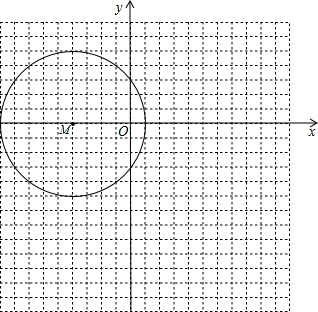
如图，在直角坐标系xOy中，每个网格的边长都是单位1，圆心为M（-4，0）的⊙M被y轴截得的弦长BC=6．
（1）求⊙M的半径长；
（2）把⊙M向下平移6个单位，再向右平移8个单位得到⊙N；请画出⊙N，观察图形写出点N的坐标，并判断⊙M与⊙N的位置关系，说明理由；
（3）画出一个“以点D（6，0）为位似中心，将⊙N缩小为原来的
”的⊙P．
查看习题详情和答案>>
（1）求⊙M的半径长；
（2）把⊙M向下平移6个单位，再向右平移8个单位得到⊙N；请画出⊙N，观察图形写出点N的坐标，并判断⊙M与⊙N的位置关系，说明理由；
（3）画出一个“以点D（6，0）为位似中心，将⊙N缩小为原来的
| 1 | 2 |
查看习题详情和答案>>
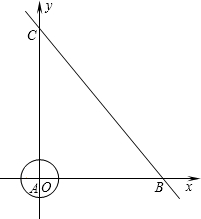如图，在直角坐标系中，半径为1的⊙A圆心与原点O重合，直线l分别交x轴、y轴于点B、点C，若点B的坐标为（6，0）且tan∠ABC=| 4 |
| 3 |
（1）若点P是⊙A上的动点，求P到直线BC的最小距离，并求此时点P的坐标；
（2）若点A从原点O出发，以1个单位/秒的速度沿着线路OB-BC-CO运动，回到点O停止运动，⊙A随着点A的运动而移动．
①求⊙A在整个运动过程中所扫过的面积；
②在⊙A整个运动过程中，⊙A与△OBC的三边相切有
6
6
种不同的情况，分别写出不同情况下，运动时间t的取值1、
、
、
、
、23
| 19 |
| 4 |
| 29 |
| 4 |
| 43 |
| 3 |
| 53 |
| 3 |
1、
、
、
、
、23
．| 19 |
| 4 |
| 29 |
| 4 |
| 43 |
| 3 |
| 53 |
| 3 |
如图，在直角坐标系xOy中，每个网格的边长都是1个单位长度，圆心为M（-4，O）的⊙M被y轴截得的弦长BC=6．
（1）求⊙M的半径长；
（2）把⊙M向下平移6个单位，再向右平移8个单位得到⊙N；请画⊙N，观察图形写出点N的坐标；请你判断⊙M与⊙N的位置关系，要说明理由；
（3）在网格图中画出一个“以点D（4，4）为位似中心，将⊙N缩小为原来的
”的⊙P．
查看习题详情和答案>>
（1）求⊙M的半径长；
（2）把⊙M向下平移6个单位，再向右平移8个单位得到⊙N；请画⊙N，观察图形写出点N的坐标；请你判断⊙M与⊙N的位置关系，要说明理由；
（3）在网格图中画出一个“以点D（4，4）为位似中心，将⊙N缩小为原来的
| 2 | 5 |
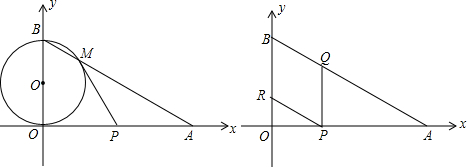
如图，在直角坐标系xOy中，O是坐标原点，点A在x正半轴上，OA=12
cm，点B在y轴的正半轴上，OB=12cm，动点P从点A开始沿AO以2
cm/s的速度向点O移动，移动时间为t s（0＜t＜6）．
（1）求∠OAB的度数；
（2）以OB为直径的⊙O′与AB交于点M，当t为何值时，PM与⊙O′相切？
（3）动点Q从点A开始沿AB以4cm/s的速度向点B移动，动点R从点B开始沿BO以2cm/s的速度向点O移动．如果P、Q、R分别从A、A、B同时移动，当t=4s时，试说明四边形BRPQ为菱形；
（4）在（3）的条件下，以R为圆心，r为半径作⊙R，当r不断变化时，⊙R与菱形BRPQ各边的交点个数将发生变化，随当交点个数发生变化时，请直接写出r的对应值或取值范围．
查看习题详情和答案>>
| 3 |
| 3 |
（1）求∠OAB的度数；
（2）以OB为直径的⊙O′与AB交于点M，当t为何值时，PM与⊙O′相切？
（3）动点Q从点A开始沿AB以4cm/s的速度向点B移动，动点R从点B开始沿BO以2cm/s的速度向点O移动．如果P、Q、R分别从A、A、B同时移动，当t=4s时，试说明四边形BRPQ为菱形；
（4）在（3）的条件下，以R为圆心，r为半径作⊙R，当r不断变化时，⊙R与菱形BRPQ各边的交点个数将发生变化，随当交点个数发生变化时，请直接写出r的对应值或取值范围．