题目内容
如图,在直角坐标系xOy中,每个网格的边长都是1个单位长度,圆心为M(-4,O)的⊙M被y轴截得的弦长BC=6.
(1)求⊙M的半径长;
(2)把⊙M向下平移6个单位,再向右平移8个单位得到⊙N;请画⊙N,观察图形写出点N的坐标;请你判断⊙M与⊙N的位置关系,要说明理由;
(3)在网格图中画出一个“以点D(4,4)为位似中心,将⊙N缩小为原来的
”的⊙P.

(1)求⊙M的半径长;
(2)把⊙M向下平移6个单位,再向右平移8个单位得到⊙N;请画⊙N,观察图形写出点N的坐标;请你判断⊙M与⊙N的位置关系,要说明理由;
(3)在网格图中画出一个“以点D(4,4)为位似中心,将⊙N缩小为原来的
| 2 | 5 |

分析:(1)根据垂径定理可可得OC=
BC=3,在Rt△MOC中利用勾股定理可得出MC,即得⊙M的半径长;
(2)根据“向下平移6个单位,再向左平移8个单位”的规律求出圆心对应点的坐标,作圆即可,根据圆心距和半径的关系可知是外切关系;
(3)利用位似图形的作图原理,找到圆心位置,以圆半径长的
为半径作圆即可.
| 1 |
| 2 |
(2)根据“向下平移6个单位,再向左平移8个单位”的规律求出圆心对应点的坐标,作圆即可,根据圆心距和半径的关系可知是外切关系;
(3)利用位似图形的作图原理,找到圆心位置,以圆半径长的
| 2 |
| 5 |
解答: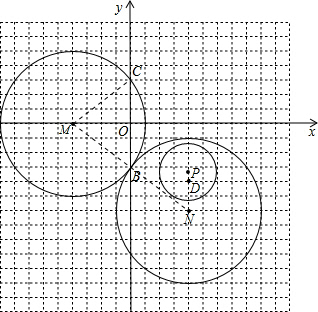 解:(1)连接MC,
解:(1)连接MC,
由垂径定理可得:OC=
BC=3,
在Rt△MOC中,MC=
=5,
即⊙M的半径长为5.
(2)⊙M与⊙N外切.
理由如下:
点M经过平移后的点N的坐标为(4,-6),
圆心距MN=10=RM+RN,
故⊙M与⊙N的位置关系为外切.
(3)所作图形如下:
 解:(1)连接MC,
解:(1)连接MC,由垂径定理可得:OC=
| 1 |
| 2 |
在Rt△MOC中,MC=
| OC2+OM2 |
即⊙M的半径长为5.
(2)⊙M与⊙N外切.
理由如下:
点M经过平移后的点N的坐标为(4,-6),
圆心距MN=10=RM+RN,
故⊙M与⊙N的位置关系为外切.
(3)所作图形如下:
点评:本题考查了圆的综合,涉及了垂径定理、圆与圆的位置关系、勾股定理及位似变换,综合性较强,注意掌握平移变换及位似变换的特点.

练习册系列答案
相关题目
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.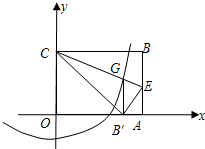 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标. 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D. 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.