题目内容
如图,在直角坐标系xOy中,每个网格的边长都是单位1,圆心为M(-4,0)的⊙M被y轴截得的弦长BC=6.(1)求⊙M的半径长;
(2)把⊙M向下平移6个单位,再向右平移8个单位得到⊙N;请画出⊙N,观察图形写出点N的坐标,并判断⊙M与⊙N的位置关系,说明理由;
(3)画出一个“以点D(6,0)为位似中心,将⊙N缩小为原来的
| 1 | 2 |
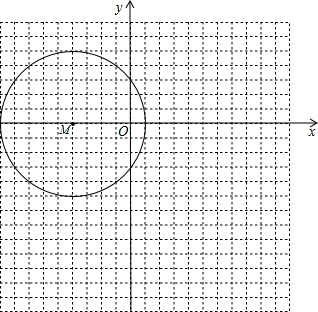
分析:(1)根据垂径定理可求得半径的长;
(2)根据“向下平移6个单位,再向右平移8个单位”的规律求出圆心对应点的坐标,作圆即可,根据圆心距和半径的关系可知是外切关系;
(3)利用位似图形的作图原理,找到圆心位置,以2.5为半径作圆即可.
(2)根据“向下平移6个单位,再向右平移8个单位”的规律求出圆心对应点的坐标,作圆即可,根据圆心距和半径的关系可知是外切关系;
(3)利用位似图形的作图原理,找到圆心位置,以2.5为半径作圆即可.
解答: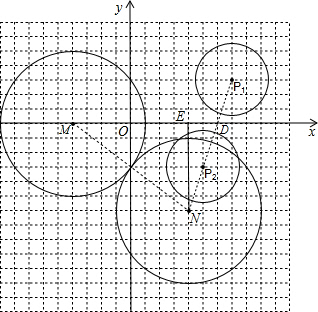 解:(1)∵MO⊥BC于点O,
解:(1)∵MO⊥BC于点O,
∴OC=
BC=3,(1分)
∴R=MC=
=5;(2分)
(2)N(4,-6),(3分)
正确画出⊙N;(4分)
⊙N与⊙M外切;(5分)
理由是:过点N作NE⊥x轴于E
∴ME=8,NE=6
∴MN=
=10=5+5=2R
∴⊙N与⊙M外切;(6分)
(3)正确画出⊙P1与⊙P2中任一个.(圆心在P1(7,3)或P2(5,-3),半径为2.5的圆.)(8分)
 解:(1)∵MO⊥BC于点O,
解:(1)∵MO⊥BC于点O,∴OC=
| 1 |
| 2 |
∴R=MC=
| 32+42 |
(2)N(4,-6),(3分)
正确画出⊙N;(4分)
⊙N与⊙M外切;(5分)
理由是:过点N作NE⊥x轴于E
∴ME=8,NE=6
∴MN=
| 82+62 |
∴⊙N与⊙M外切;(6分)
(3)正确画出⊙P1与⊙P2中任一个.(圆心在P1(7,3)或P2(5,-3),半径为2.5的圆.)(8分)
点评:本题考查的是平移变换与位似变换作图.
作平移图形时,找关键点的对应点也是关键的一步.平移作图的一般步骤为:①确定平移的方向和距离,先确定一组对应点;②确定图形中的关键点;③利用第一组对应点和平移的性质确定图中所有关键点的对应点;④按原图形顺序依次连接对应点,所得到的图形即为平移后的图形.
作位似变换的图形的依据是相似的性质,基本作法是①先确定图形的位似中心;②利用相似图形的比例关系作出关键点的对应点;③按原图形中的方式顺次连接对应点.要注意有两种情况,图形在位似中心的同侧或在位似中心的两侧.
作平移图形时,找关键点的对应点也是关键的一步.平移作图的一般步骤为:①确定平移的方向和距离,先确定一组对应点;②确定图形中的关键点;③利用第一组对应点和平移的性质确定图中所有关键点的对应点;④按原图形顺序依次连接对应点,所得到的图形即为平移后的图形.
作位似变换的图形的依据是相似的性质,基本作法是①先确定图形的位似中心;②利用相似图形的比例关系作出关键点的对应点;③按原图形中的方式顺次连接对应点.要注意有两种情况,图形在位似中心的同侧或在位似中心的两侧.

练习册系列答案
相关题目
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.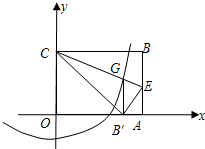 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标. 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D. 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.