题目内容
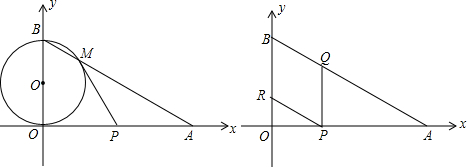
如图,在直角坐标系xOy中,O是坐标原点,点A在x正半轴上,OA=12
cm,点B在y轴的正半轴上,OB=12cm,动点P从点A开始沿AO以2
cm/s的速度向点O移动,移动时间为t s(0<t<6).
(1)求∠OAB的度数;
(2)以OB为直径的⊙O′与AB交于点M,当t为何值时,PM与⊙O′相切?
(3)动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从A、A、B同时移动,当t=4s时,试说明四边形BRPQ为菱形;
(4)在(3)的条件下,以R为圆心,r为半径作⊙R,当r不断变化时,⊙R与菱形BRPQ各边的交点个数将发生变化,随当交点个数发生变化时,请直接写出r的对应值或取值范围.
| 3 |
| 3 |
(1)求∠OAB的度数;
(2)以OB为直径的⊙O′与AB交于点M,当t为何值时,PM与⊙O′相切?
(3)动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从A、A、B同时移动,当t=4s时,试说明四边形BRPQ为菱形;
(4)在(3)的条件下,以R为圆心,r为半径作⊙R,当r不断变化时,⊙R与菱形BRPQ各边的交点个数将发生变化,随当交点个数发生变化时,请直接写出r的对应值或取值范围.

分析:(1)在Rt△OAB中,已知了OA、OB的长,即可求出∠OAB的正切值,由此可得到∠OAB的度数;
(2)连接O′M,当PM与⊙O′相切时,PM、PO同为⊙O′的切线,易证得△OO′P≌△MO′P,则∠OO′P=∠MO′P;在(1)中易得∠OBA=60°,即△O′BM是等边三角形,由此可得到∠BO′M=∠PO′M=∠PO′O=60°;在Rt△OPO′中,根据∠PO′O的度数及OO′的长即可求得OP的长,已知了P点的运动速度,即可根据时间=路程÷速度求得t的值;
(3)分别求得BR、AP、BR的长,依据依据平行线分线段成比例定理的逆定理即可证得四边形BRPQ是平行四边形,然后在直角三角形OPR中,利用勾股定理求得BR的长,从而证明BR=PR,即可证得;
(4)根据(3)可以得到四边形BRPQ是菱形,则△BPQ是等边三角形,据此即可求得R到四边形的边的距离,从而判断.
(2)连接O′M,当PM与⊙O′相切时,PM、PO同为⊙O′的切线,易证得△OO′P≌△MO′P,则∠OO′P=∠MO′P;在(1)中易得∠OBA=60°,即△O′BM是等边三角形,由此可得到∠BO′M=∠PO′M=∠PO′O=60°;在Rt△OPO′中,根据∠PO′O的度数及OO′的长即可求得OP的长,已知了P点的运动速度,即可根据时间=路程÷速度求得t的值;
(3)分别求得BR、AP、BR的长,依据依据平行线分线段成比例定理的逆定理即可证得四边形BRPQ是平行四边形,然后在直角三角形OPR中,利用勾股定理求得BR的长,从而证明BR=PR,即可证得;
(4)根据(3)可以得到四边形BRPQ是菱形,则△BPQ是等边三角形,据此即可求得R到四边形的边的距离,从而判断.
解答: 解:(1)在Rt△AOB中:
解:(1)在Rt△AOB中:
tan∠OAB=
=
=
,
∴∠OAB=30°.
(2)如图,连接O′P,O′M.
当PM与⊙O′相切时,有:
∠PMO′=∠POO′=90°,
△PMO′≌△POO′.
由(1)知∠OBA=60°,
∵O′M=O′B,
∴△O′BM是等边三角形,
∴∠BO′M=60°.
可得∠OO′P=∠MO′P=60°.
∴OP=OO′•tan∠OO′P=6tan60°=6
.
又∵OP=2
t
∴AP=6
∴2
t=6
,
∴t=3.
即:t=3时,PM与⊙O′相切;
(3)当t=4s时,AQ=4×4=16,
BR=2×4=8,AP=4×2
=8
,
∴
=
,
∴PR∥AB,
同理,QP∥BR,
∴四边形BRPQ是平行四边形,
在直角△OPR中,OP=OA-AP=12
-8
=4
,OR=OB-BR=12-8=4,
PR=
=
=8,
∴BR=PR,
∴平行四边形BRPQ是菱形;
(4)∵四边形BRPQ是菱形时,根据(1)可以得到∠OBA=60°,
∴RB=RQ=RP=8,△BPQ是等边三角形,
∴R到BQ和PQ的距离都是:8×
=4
,
故当0<r<4
时,有2个交点;
当r=4
时,有4个交点;
当4
<r<8时,有6个交点;
当r=8时,有3个交点;
当r>8时,有0个交点.
 解:(1)在Rt△AOB中:
解:(1)在Rt△AOB中:tan∠OAB=
| OB |
| OA |
| 12 | ||
12
|
| ||
| 3 |
∴∠OAB=30°.
(2)如图,连接O′P,O′M.
当PM与⊙O′相切时,有:
∠PMO′=∠POO′=90°,
△PMO′≌△POO′.
由(1)知∠OBA=60°,
∵O′M=O′B,
∴△O′BM是等边三角形,
∴∠BO′M=60°.
可得∠OO′P=∠MO′P=60°.
∴OP=OO′•tan∠OO′P=6tan60°=6
| 3 |
又∵OP=2
| 3 |
∴AP=6
| 3 |
∴2
| 3 |
| 3 |
∴t=3.
即:t=3时,PM与⊙O′相切;
(3)当t=4s时,AQ=4×4=16,
BR=2×4=8,AP=4×2
| 3 |
| 3 |
∴
| OR |
| OB |
| OP |
| OA |
∴PR∥AB,
同理,QP∥BR,
∴四边形BRPQ是平行四边形,
在直角△OPR中,OP=OA-AP=12
| 3 |
| 3 |
| 3 |
PR=
| OP2+OR2 |
(4
|
∴BR=PR,
∴平行四边形BRPQ是菱形;
(4)∵四边形BRPQ是菱形时,根据(1)可以得到∠OBA=60°,
∴RB=RQ=RP=8,△BPQ是等边三角形,
∴R到BQ和PQ的距离都是:8×
| ||
| 2 |
| 3 |
故当0<r<4
| 3 |
当r=4
| 3 |
当4
| 3 |
当r=8时,有3个交点;
当r>8时,有0个交点.
点评:本题考查了切线的性质,菱形的判定方法,以及勾股定理,正确证明四边形BRPQ是菱形是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.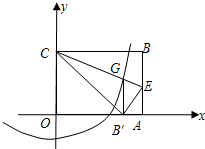 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标. 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D. 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.