Question

如图，在直角坐标系中，一次函数y=

3

3

x+2的图象与x轴交于点A，与y轴交于点B
①若以原点为圆心的圆与直线相切于点C，求C点的坐标；
②在⊙O中剪掉扇形COD后，求剩下的部分做成的圆锥的底面半径（结果用根号表示）．
③在x轴上是否存在这样的点P，使△PAB为等腰三角形？若存在请写出点P坐标；若不存在请说明原因．

Answer 1

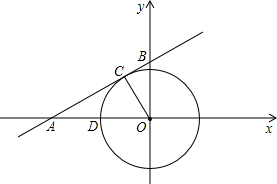
分析：由已知以原点为圆心的圆与直线相切于点C可求出直线OC，从而求出C点的坐标，再由C点的坐标可以求出OC（半径）及∠COD，既而求出在⊙O中剪掉扇形COD后，求剩下的部分做成的圆锥的底面半径．由一次函数y=

3

3

x+2的图象与x轴交于点A，与y轴交于点B，可求出点A和B，由直角坐标系可知，构成的等腰三角形有四种情况：以A为顶点两个，以B为顶点一个，以P为顶点一个，根据两点的距离公式可求出每种情况的点P的坐标．

解答：解：①已知以原点为圆心的圆与直线相切于点C，
∴直线OC的截距k=-1÷

3

3

=-

3

，
∴直线OC的方程为：y=-

3

x，
解

3

3

x+2=-

3

x，
得x=-

3

2

，代入y=-

3

x得：y=

3

2

，
所以C点的坐标为（-

3

2

，

3

2

）．

②已知C点的坐标为（-

3

2

，

3

2

），
∴OC²=(

3

2

)2+(

3

2

)2=3，
OC=

3

，
∴tan∠COD=

3

2

÷

3

2

=

3

，
∴∠COD=60°，
∴在⊙O中剪掉扇形COD后，剩下的部分做成的圆锥的底面半径为：
2π•

3

•

360-60

360

÷（2π）=

5 3

6

．

③存在，分别是p1(2

3

，0)，p 2(4-2

3

，0)，p3(-4-2

3

，0)，p4(-

2 3

3

，0)．

点评：此题是一次函数和圆、切线、等腰三角形综合题，解题的关键是①由已知切线确定直线OC的方程求C点的坐标．②再由C点的坐标求出半径和剪去的角，从而求出圆锥的半径．③由已知先求出点A和B，再由直角坐标系确定构成等腰三角形的情况．