摘要：已知F为抛物线 的焦点.点P在该抛物线上移动.又点M(1.1).为使得取得最小值.则P点坐标为(***)
网址：http://m.1010jiajiao.com/timu_id_558651[举报]
第1卷
一、选择题（每小题5分，满分50分。）
题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
A
D
C
D
B
C
A
D
二、填空题（每小题2分，满分10分。）
11. 13 12. 
三、解答题（4题，满分40分）
13． m ≥ 3 或 1 < m ≤ 2
14． （1）
（2） 
15． （1）
（2）最大值 
；最小值 
16. （1）A（－2 ，1）、 B（4， 4） （2）P（ 1，
） ，
第2卷
17、 6 18、 4 19、 D 20、 C
21．（1）a = 16 ； （2）增区间：（－1，1），（3，+∞）；减区间：（1，3）
22．（1）
（2）
已知点A（4，4）在抛物线y2=px（p＞0）上，该抛物线的焦点为F，过点A作直线l：x=-
的垂线，垂足为M，则∠MAF的平分线所在直线的方程为
查看习题详情和答案>>
| p | 4 |
x-2y+4=0
x-2y+4=0
．已知抛物线C：y2=2px（p＞0）上任意一点到焦点F的距离比到y轴的距离大1．
（1）求抛物线C的方程；
（2）若过焦点F的直线交抛物线于M、N两点，M在第一象限，且|MF|=2|NF|，求直线MN的方程；
（3）求出一个数学问题的正确结论后，将其作为条件之一，提出与原来问题有关的新问题，我们把它称为原来问题的一个“逆向”问题．
例如，原来问题是“若正四棱锥底面边长为4，侧棱长为3，求该正四棱锥的体积”．求出体积
后，它的一个“逆向”问题可以是“若正四棱锥底面边长为4，体积为
，求侧棱长”；也可以是“若正四棱锥的体积为
，求所有侧面面积之和的最小值”．
现有正确命题：过点A(-
，0)的直线交抛物线C：y2=2px（p＞0）于P、Q两点，设点P关于x轴的对称点为R，则直线RQ必过焦点F．
试给出上述命题的“逆向”问题，并解答你所给出的“逆向”问题．
查看习题详情和答案>>
（1）求抛物线C的方程；
（2）若过焦点F的直线交抛物线于M、N两点，M在第一象限，且|MF|=2|NF|，求直线MN的方程；
（3）求出一个数学问题的正确结论后，将其作为条件之一，提出与原来问题有关的新问题，我们把它称为原来问题的一个“逆向”问题．
例如，原来问题是“若正四棱锥底面边长为4，侧棱长为3，求该正四棱锥的体积”．求出体积
| 16 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
现有正确命题：过点A(-
| p |
| 2 |
试给出上述命题的“逆向”问题，并解答你所给出的“逆向”问题．
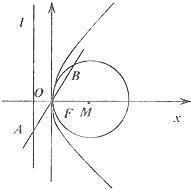已知抛物线C：y2=2px（p＞0）的准线为l，焦点为F，⊙M的圆心在x轴的正半轴上，且与y轴相切，过原点O作倾斜角为