题目内容
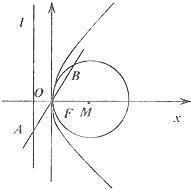 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,⊙M的圆心在x轴的正半轴上,且与y轴相切,过原点O作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,⊙M的圆心在x轴的正半轴上,且与y轴相切,过原点O作倾斜角为| π | 3 |
(1)求⊙M和抛物线C的方程;
(2)过l上的动点Q向⊙M作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
分析:(1)根据
=OA•cos60°可求出p的值,从而求出抛物线方程,求出圆心和半径可求出⊙M的方程;
(2)以点Q为圆心,QS为半径作⊙Q,则线段ST即为⊙Q与⊙M的公共弦,求出⊙Q的方程,可得ST的方程,从而可求定点坐标.
| p |
| 2 |
(2)以点Q为圆心,QS为半径作⊙Q,则线段ST即为⊙Q与⊙M的公共弦,求出⊙Q的方程,可得ST的方程,从而可求定点坐标.
解答:(1)解:因为
=OA•cos60°=2×
=1,即p=2,所以抛物线C的方程为y2=4x
设⊙M的半径为r,则r=
×
=2,所以⊙M的方程为(x-2)2+y2=4;
(2)证明:以点Q为圆心,QS为半径作⊙Q,则线段ST即为⊙Q与⊙M的公共弦
设点Q(-1,t),则QS2=QM2-4=t2+5,
所以⊙Q的方程为(x+1)2+(y-t)2=t2+5
从而直线ST的方程为3x-ty-2=0(*)
因为x=
,y=0一定是方程(*)的解,所以直线ST恒过一个定点,且该定点坐标为(
,0).
| p |
| 2 |
| 1 |
| 2 |
设⊙M的半径为r,则r=
| OB |
| 2 |
| 1 |
| cos60° |
(2)证明:以点Q为圆心,QS为半径作⊙Q,则线段ST即为⊙Q与⊙M的公共弦
设点Q(-1,t),则QS2=QM2-4=t2+5,
所以⊙Q的方程为(x+1)2+(y-t)2=t2+5
从而直线ST的方程为3x-ty-2=0(*)
因为x=
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题主要考查了圆的方程和抛物线方程,考查直线恒过定点问题,确定ST是⊙Q与⊙M的公共弦是关键.

练习册系列答案
相关题目
 如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点). 已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.
已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.