题目内容
已知点A(4,4)在抛物线y2=px(p>0)上,该抛物线的焦点为F,过点A作直线l:x=-
的垂线,垂足为M,则∠MAF的平分线所在直线的方程为
| p | 4 |
x-2y+4=0
x-2y+4=0
.分析:先求出抛物线方程,再抛物线的定义可得|AF|=|AM|,所以∠MAF的平分线所在直线就是线段MF的垂直平分线,从而可得结论.
解答:解:∵点A(4,4)在抛物线y2=px(p>0)上,∴16=4p,∴p=4
∴抛物线的焦点为F(1,0),准线方程为x=-1,M(-1,4)
由抛物线的定义可得|AF|=|AM|,所以∠MAF的平分线所在直线就是线段MF的垂直平分线
∵kMF=
=-2,
∴∠MAF的平分线所在直线的方程为y-4=
(x-4),即x-2y+4=0
故答案为:x-2y+4=0
∴抛物线的焦点为F(1,0),准线方程为x=-1,M(-1,4)
由抛物线的定义可得|AF|=|AM|,所以∠MAF的平分线所在直线就是线段MF的垂直平分线
∵kMF=
| 4-0 |
| -1-1 |
∴∠MAF的平分线所在直线的方程为y-4=
| 1 |
| 2 |
故答案为:x-2y+4=0
点评:本题考查抛物线的标准方程,考查学生的计算能力,属于基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
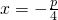 的垂线,垂足为M,则∠MAF的平分线所在直线的方程为________.
的垂线,垂足为M,则∠MAF的平分线所在直线的方程为________. 的垂线,垂足为M,则∠MAF的平分线所在直线的方程为 .
的垂线,垂足为M,则∠MAF的平分线所在直线的方程为 .