摘要：若点G与C1重合. 平面ADG即B1C1与AD确定的平面.∴B1C1平面ADG若点G与C1不重合
网址：http://m.1010jiajiao.com/timu_id_546137[举报]
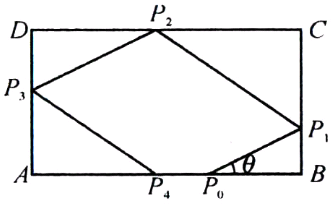（2012•泰州二模）如图，矩形ABCD中，AB=3，AD=2，一质点从AB边上的点P0出发，沿与AB的夹角为θ的方向射到边BC上点P1后，依次反射（入射角与反射角相等）到边CD，DA和AB上的点P2，P3，P4处．（1）若点P4与P0重合，求tanθ的值；
（2）设tanθ=t，若P4落在A，P0两点之间，且AP0=2．将五边形P0P1P2P3P4的面积S表示为t的函数，并求S的最大值．
在空间直角坐标系O-xyz中，方程
+
+
=1(a＞b＞c＞0)表示中心在原点、其轴与坐标轴重合的某椭球面的标准方程．2a，2b，2c分别叫做椭球面的长轴长，中轴长，短轴长．类比在平面直角坐标系中椭圆标准方程的求法，在空间直角坐标系O-xyz中，若椭球面的中心在原点、其轴与坐标轴重合，平面xOy截椭球面所得椭圆的方程为
+
=1，且过点M(1，2，
)，则此椭球面的标准方程为
+
+
=1
+
+
=1．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| z2 |
| c2 |
| x2 |
| 9 |
| y2 |
| 16 |
| 23 |
| x2 |
| 9 |
| y2 |
| 16 |
| z2 |
| 36 |
| x2 |
| 9 |
| y2 |
| 16 |
| z2 |
| 36 |
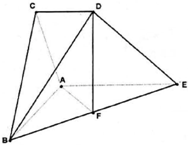如图所示的几何体中，△ABC为正三角形，AE和CD都垂直于平面ABC，且AE=AB=2，CD=1，F为BE的中点．（1）若点G在AB上，试确定G点位置，使FG∥平面ADE，并加以证明；
（2）求DB与平面ABE所成角的正弦值． 查看习题详情和答案>>
中，方程
表示中心在原点、其轴与坐标轴重合的某椭球面的标准方程．
分别叫做椭球面的长轴长，中轴长，短轴长．类比在平面直角坐标系中椭圆标准方程的求法，在空间直角坐标系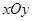
截椭球面所得椭圆的方程为
，且过点M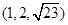
,则此椭球面的标准方程为________