Question

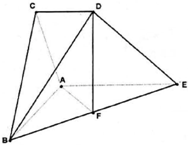如图所示的几何体中，△ABC为正三角形，AE和CD都垂直于平面ABC，且AE=AB=2，CD=1，F为BE的中点．
（1）若点G在AB上，试确定G点位置，使FG∥平面ADE，并加以证明；
（2）求DB与平面ABE所成角的正弦值．

Answer 1

分析：（1）当G是AB的中点时，GF∥平面ADE．G是AB的中点，F是BE的中点?GF∥AE?FG∥平面ADE；
（2）先根据（1）的结论得四边形CDFG为平行四边形以及根据AE⊥CG；再借助于△ABC为正三角形，G为AB中点得到CG⊥AB；进而得到∠DBF为所求线面角；然后在RT△DBF中根据边长求出∠DBF的正弦值即可．

解答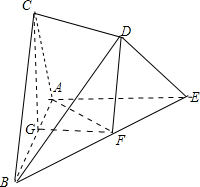：解：（1）当G是AB的中点时，GF∥平面ADE．
证明：因为G是AB的中点，F是BE的中点．
所以GF∥AE．
又GF?平面ADE．AE⊆平面ADE．
∴GF∥平面ADE．
（2）连接CG．由（1）可知：GF∥AE且GF=

1

2

AE．
又AE⊥平面ABC，CD⊥平面ABC．
所以CD∥AE，CD=

1

2

AE．
∴CD∥GF，GF=CD
∴四边形CDFG为平行四边形．
∴DF∥CG且DF=CG．
又因为AE⊥平面ABC，CG⊆平面ABC．
所以AE⊥CG．
∵△ABC为正三角形，G为AB中点．
∴CG⊥AB．
∴DF⊥AE且DF⊥AB．
∴DF⊥面ABE
所以∠DBF为所求线面角．
又DF=AG=

3

，DB=

5

，
∴sin∠DBF=

15

5

．

点评：本题主要考查线面平行的证明以及线面所成角的求法．在证明线面平行时，一般先证线线平行或面面平行．