题目内容
如图,在Rt△ABC中,AB=BC=4,点£在线段AB上.过点E作EF∥BC交AC于点F,将△AEF沿EF折起到△PEF的位置(点A与P重合),使得∠PEB=60°.(I )求证:EF丄PB;
(II )试问:当点E在线段AB上移动时,二面角P-FC-B的平面角的余弦值是否为定值?若是,求出其定值;若不是,说明理由.
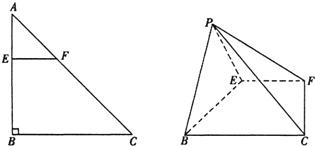
分析:(I)由已知在Rt△ABC中,中EF∥BC,我们可得到EF⊥AB,即EF⊥EB,EF⊥EP,由线面垂直的判定定理定理,易得EF⊥平面PEB,再由线面垂直的定义,即可得到EF丄PB;
(II )在平面PEB中,过P点作PD⊥BE于D,结合(I)的结论可得BH⊥平面BCFE,以B为坐标原点,BC,BE,BH方向分别为X,Y,Z轴正方向建立空间坐标系,则我们可以分别求出平面PFC与平面BFC的法向量,代入二面角的向量夹角公式中,求出其余弦值,判断后,即可得到答案.
(II )在平面PEB中,过P点作PD⊥BE于D,结合(I)的结论可得BH⊥平面BCFE,以B为坐标原点,BC,BE,BH方向分别为X,Y,Z轴正方向建立空间坐标系,则我们可以分别求出平面PFC与平面BFC的法向量,代入二面角的向量夹角公式中,求出其余弦值,判断后,即可得到答案.
解答:解:(I)证明:在Rt△ABC中,∵EF∥BC
∴EF⊥AB
∴EF⊥EB,EF⊥EP,又由EB∩EP=E
∴EF⊥平面PEB
又∵PB?平面PEB
∴EF⊥PB
(II)在平面PEB中,过P点作PD⊥BE于D,
由(I)知,EF⊥PD
∴PD⊥平面BCFE
在平面PEB中过点B作直线BH∥PD
则BH⊥平面BCFE
如图,以B为坐标原点,BC,BE,BH方向分别为X,Y,Z轴正方向建立空间坐标系,
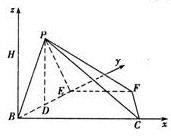 设PE=x(0<x<4),又∵AB=BC=4
设PE=x(0<x<4),又∵AB=BC=4
∴BE=4-x,EF=x
在Rt△PED中,∠PED=60°
∴PD=
x,DE=
x
∴BD=4-x-
x=4-
x
∴C(4,0,0),F(x,4-x,0),P(0,4-
x,
x)
从而
=(x-4,4-x,0),
=(-4,4-
x,
x)
设
=(a,b,c)是平面PCF的一个法向量,则:
即
令b=1,则
=(1,1,
)是平面PCF的一个法向量,
又∵平面BCF的一个法向量为
=(0,0,1)
设二面角P-FC-B的平面角为θ,则
Cosθ=
=
∴当点E在线段AB上移动时,二面角P-FC-B的平面角的余弦值为定值
∴EF⊥AB
∴EF⊥EB,EF⊥EP,又由EB∩EP=E
∴EF⊥平面PEB
又∵PB?平面PEB
∴EF⊥PB
(II)在平面PEB中,过P点作PD⊥BE于D,
由(I)知,EF⊥PD
∴PD⊥平面BCFE
在平面PEB中过点B作直线BH∥PD
则BH⊥平面BCFE
如图,以B为坐标原点,BC,BE,BH方向分别为X,Y,Z轴正方向建立空间坐标系,
 设PE=x(0<x<4),又∵AB=BC=4
设PE=x(0<x<4),又∵AB=BC=4∴BE=4-x,EF=x
在Rt△PED中,∠PED=60°
∴PD=
| ||
| 2 |
| 1 |
| 2 |
∴BD=4-x-
| 1 |
| 2 |
| 3 |
| 2 |
∴C(4,0,0),F(x,4-x,0),P(0,4-
| 3 |
| 2 |
| ||
| 2 |
从而
| CF |
| CP |
| 3 |
| 2 |
| ||
| 2 |
设
| n |
|
即
|
令b=1,则
| n |
| 3 |
又∵平面BCF的一个法向量为
| v |
设二面角P-FC-B的平面角为θ,则
Cosθ=
| ||||
|
|
| ||
| 5 |
∴当点E在线段AB上移动时,二面角P-FC-B的平面角的余弦值为定值
| ||
| 5 |
点评:本题主要考查直线与直线,直线与平面、平面与平面的位置关系等基础知识,考查空间想像能力、推理论证能力、运算求解能力、考查化归与转化思想,函数与方程思想等.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2
如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2| 3 |
A、2
| ||||
| B、3 | ||||
C、
| ||||
D、
|
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E. 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P. 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=