摘要:设与交于点由.得
网址:http://m.1010jiajiao.com/timu_id_544272[举报]
设A是单位圆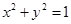 上任意一点,
上任意一点, 是过点
是过点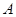 与
与 轴垂直的直线,
轴垂直的直线,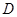 是直线
是直线 与
与 轴的交点,点
轴的交点,点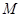 在直线
在直线 上,且满足
上,且满足 ,当点
,当点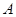 在圆上运动时,记点
在圆上运动时,记点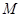 的轨迹为曲线
的轨迹为曲线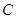 。
。
(1)求曲线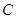 的方程,判断曲线
的方程,判断曲线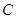 为何种圆锥曲线,并求其焦点坐标。
为何种圆锥曲线,并求其焦点坐标。
(2)过原点斜率为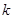 的直线交曲线
的直线交曲线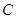 于
于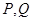 两点,其中
两点,其中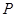 在第一象限,且它在
在第一象限,且它在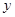 轴上的射影为点
轴上的射影为点 ,直线
,直线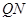 交曲线
交曲线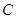 于另一点
于另一点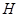 ,是否存在
,是否存在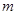 ,使得对任意的
,使得对任意的 ,都有
,都有 ?若存在,请说明理由。
?若存在,请说明理由。
查看习题详情和答案>>
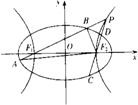
如图,已知椭圆E:
+
=1(a>b>0),焦点为F1、F2,双曲线G:x2-y2=m(m>0)的顶点是该椭圆的焦点,设P是双曲线G上异于顶点的任一点,直线PF1、PF2与椭圆的交点分别为A、B和C、D,已知三角形ABF2的周长等于8
,椭圆四个顶点组成的菱形的面积为8
.
(1)求椭圆E与双曲线G的方程;
(2)设直线PF1、PF2的斜率分别为k1和k2,探求k1和k2的关系;
(3)是否存在常数λ,使得|AB|+|CD|=λ|AB|•|CD|恒成立?若存在,试求出λ的值;若不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
(1)求椭圆E与双曲线G的方程;
(2)设直线PF1、PF2的斜率分别为k1和k2,探求k1和k2的关系;
(3)是否存在常数λ,使得|AB|+|CD|=λ|AB|•|CD|恒成立?若存在,试求出λ的值;若不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
 如图,抛物线C1:y2=4x的焦点到准线的距离与椭圆C2:
如图,抛物线C1:y2=4x的焦点到准线的距离与椭圆C2:| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
(1)求椭圆C2的标准方程;
(2)过点A作直线l交C1于C,D两点,射线OC,OD分别交C2于E,F两点.
(I)求证:O点在以EF为直径的圆的内部;
(II)记△OEF,△OCD的面积分别为S1,S2,问是否存在直线l,使得S2=3S1?请说明理由.
 如图,已知椭圆
如图,已知椭圆