题目内容
 如图,抛物线C1:y2=4x的焦点到准线的距离与椭圆C2:
如图,抛物线C1:y2=4x的焦点到准线的距离与椭圆C2:| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
(1)求椭圆C2的标准方程;
(2)过点A作直线l交C1于C,D两点,射线OC,OD分别交C2于E,F两点.
(I)求证:O点在以EF为直径的圆的内部;
(II)记△OEF,△OCD的面积分别为S1,S2,问是否存在直线l,使得S2=3S1?请说明理由.
分析:(1)p=2,得椭圆的长半轴a=2,由S△OAB=
×|OA|×yB=
,知yB=
.代入抛物线能求出椭圆C2方程.
(2)(I)设直线l的方程为:x=my+2,由
,得y2-4my-8=0,利用韦达定理和向量的数量积导出∠COD>90°,由此能证明O点在以EF为直径的圆的内部.
(II)
=
=
•
,直线OC的斜率为
=
,故直线OC的方程为x=
.由此能推导出不存在直线l使得S2=3S1
| 1 |
| 2 |
2
| ||
| 3 |
2
| ||
| 3 |
(2)(I)设直线l的方程为:x=my+2,由
|
(II)
| S1 |
| S2 |
| ||
|
| |y1| |
| |yE| |
| |y2| |
| |yF| |
| y1 |
| x1 |
| 4 |
| y1 |
| y1•y |
| 4 |
解答:解:(1)p=2,得椭圆的长半轴a=2,
∵S△OAB=
×|OA|×yB=
,
∴yB=
.
代入抛物线求得B(
,
),
∴椭圆C2方程为:
+
=1.
(2)(I)设直线l的方程为:x=my+2,
由
,得y2-4my-8=0,
设C(x1,y1),D(x2,y2),
∴y1+y2=4m,y1y2=-8,
∴x1x2=4,
∴
•
=x1x2+y1y2=-4<0,
∴∠COD>90°,
又∵∠EOF=∠COD,
∴∠EOF>90°,
∴O点在以EF为直径的圆的内部.
(II)
=
=
•
,
直线OC的斜率为
=
,
∴直线OC的方程为x=
.
由
,
得yE2=
,yF2=
,
∴yE2•yF2=
,
∴(
)2=
,
∵m∈R,∴
≥
∴
≥
>3,
∴不存在直线l使得S2=3S1.
∵S△OAB=
| 1 |
| 2 |
2
| ||
| 3 |
∴yB=
2
| ||
| 3 |
代入抛物线求得B(
| 2 |
| 3 |
2
| ||
| 3 |
∴椭圆C2方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(2)(I)设直线l的方程为:x=my+2,
由
|
设C(x1,y1),D(x2,y2),
∴y1+y2=4m,y1y2=-8,
∴x1x2=4,
∴
| OC |
| OD |
∴∠COD>90°,
又∵∠EOF=∠COD,
∴∠EOF>90°,
∴O点在以EF为直径的圆的内部.
(II)
| S1 |
| S2 |
| ||
|
| |y1| |
| |yE| |
| |y2| |
| |yF| |
直线OC的斜率为
| y1 |
| x1 |
| 4 |
| y1 |
∴直线OC的方程为x=
| y1•y |
| 4 |
由
|
得yE2=
| 64×3 |
| 3y12+64 |
| 64×3 |
| 3y22+64 |
∴yE2•yF2=
| 64×32 |
| 121+48m |
∴(
| S2 |
| S1 |
| 121+48m2 |
| 32 |
∵m∈R,∴
| 121+48m2 |
| 32 |
| 112 |
| 32 |
| S2 |
| S1 |
| 11 |
| 3 |
∴不存在直线l使得S2=3S1.
点评:本题考查椭圆方程的求法,考查点在圆的内部的证明,探索满足条件的直线方程是否存在.综合性强,难度大,对数学思维的要求较高.解题时要认真审题,仔细解答,注意等价转化思想的合理合理运用.

练习册系列答案
相关题目
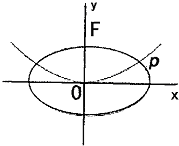 如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2: (2012•河北模拟)如图,抛物线C1:y2=2px(p>0)的焦点为F,A为C1上的点,以F为圆心,
(2012•河北模拟)如图,抛物线C1:y2=2px(p>0)的焦点为F,A为C1上的点,以F为圆心, 的离心率
的离心率 ,C1与C2在第一象限的交点为
,C1与C2在第一象限的交点为 ,
, 。
。 
 如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1-
如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1-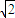 时,切线MA的斜率为-
时,切线MA的斜率为- .
.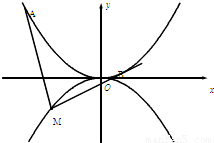 如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1-
如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1- 时,切线MA的斜率为-
时,切线MA的斜率为- .
.