��Ŀ����
��ͼ����֪��ԲE��| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
��1������ԲE��˫����G�ķ��̣�
��2����ֱ��PF1��PF2��б�ʷֱ�Ϊk1��k2��̽��k1��k2�Ĺ�ϵ��
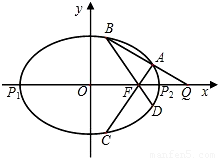
��3���Ƿ���ڳ����ˣ�ʹ��|AB|+|CD|=��|AB|•|CD|������������ڣ�������˵�ֵ���������ڣ���˵�����ɣ�

��������1������������ABF2���ܳ�����8
����Բ�ĸ�������ɵ����ε����Ϊ8
�����a��b��ֵ��������˫����G��x2-y2=m��m��0���Ķ����Ǹ���Բ�Ľ�����������m��ֵ��
��2��������б�ʹ�ʽk=
��ʾ��k1��k2��̽��k1��k2�Ĺ�ϵ����ϵ�Ǿ��Ǻͣ�������̣�
��3��ǣ�浽|AB|��|CD|��|AB|��|CD|���õ��ҳ���ʽ�������Ҫ�������̣�����Ҫ��ֱ��AB�ķ���������������̴�����㼴�ɣ�
| 2 |
| 2 |
��2��������б�ʹ�ʽk=
| y2-y1 |
| x2-x1 |
��3��ǣ�浽|AB|��|CD|��|AB|��|CD|���õ��ҳ���ʽ�������Ҫ�������̣�����Ҫ��ֱ��AB�ķ���������������̴�����㼴�ɣ�
����⣺��1��������֪����Բ��4a=8
��a=2
��2ab=8
��b=2
������Բ�ı�����Ϊ
+
=1
�ֶ����뽹���غϣ�����m=c2=a2-b2=4��
���Ը�˫���ߵı�����Ϊ
-
=1��
��2�����P��x��y����x�١�2k1=
��k2=
k1•k2=
P��˫�����ϣ�����
-
=1y2=x2-4����k1•k2=1
��3����ֱ��AB��y=k1��x+2��k1��0
�ɷ�����
�ã�2k12+1��x2+8k12x+8k12-8=0
��A��x1��y1����B��x2��y2��
����x1+x2=
��x1x2=
���ҳ���ʽ|AB|=
=
ͬ��|CD|=
=
��k1•k2=1��k2=
�����|CD|=
|AB|+|CD|=��|AB|CD|����=
+
=
���Դ�����=
ʹ��|AB|+|CD|=��|AB|CD|������
| 2 |
| 2 |
| 2 |
������Բ�ı�����Ϊ
| x2 |
| 8 |
| y2 |
| 4 |
�ֶ����뽹���غϣ�����m=c2=a2-b2=4��
���Ը�˫���ߵı�����Ϊ
| x2 |
| 4 |
| y2 |
| 4 |
��2�����P��x��y����x�١�2k1=
| y |
| x+2 |
| y |
| x-2 |
| y2 |
| x2-4 |
P��˫�����ϣ�����
| x2 |
| 4 |
| y2 |
| 4 |
��3����ֱ��AB��y=k1��x+2��k1��0
�ɷ�����
|
��A��x1��y1����B��x2��y2��
����x1+x2=
| -8k12 |
| 2k12+1 |
| 8k12-8 |
| 2k12+1 |
���ҳ���ʽ|AB|=
| 1+k12 |
| (x1+x2)2-4x1x2 |
4
| ||
| 2k12+1 |
ͬ��|CD|=
| 1+k22 |
| (x1+x2)2-4x1x2 |
4
| ||
| 2k22+1 |
��k1•k2=1��k2=
| 1 |
| k1 |
4
| ||
| k12+2 |
| 1 |
| |AB| |
| 1 |
| |CD| |
3
| ||
| 8 |
���Դ�����=
3
| ||
| 8 |
�����������һ�ʽϼ����������ڶ��ʽϸ��ӣ�һ������µĹ�ϵ�Ǿ��Ǻͣ�������̣��ؼ���P��˫�����ϣ�����
-
=1y2=x2-4Ȼ�������㣮��������ƽ���ϳ��������ͣ���Ҫ�Ǽ��㷱����ֻҪ���㲻���������ԴﵽĿ�ģ�
| x2 |
| 4 |
| y2 |
| 4 |

��ϰ��ϵ�д�
�����Ŀ
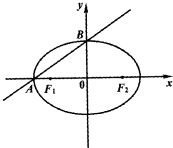
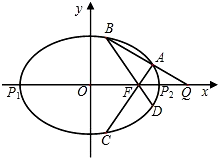 ��2013•������ģ����ͼ����֪��ԲE��
��2013•������ģ����ͼ����֪��ԲE��




 ��
��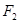 ��x���ϣ�������
��x���ϣ�������
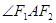 �Ľ�ƽ��������ֱ��
�Ľ�ƽ��������ֱ��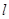 �ķ���.
�ķ���.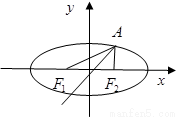
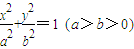 ����������
����������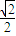 ��P1��P2����ԲE�ij���������˵㣨P2λ��P1�Ҳࣩ����F����ԲE���ҽ��㣮��Q��x����λ��P2�Ҳ��һ�㣬������
��P1��P2����ԲE�ij���������˵㣨P2λ��P1�Ҳࣩ����F����ԲE���ҽ��㣮��Q��x����λ��P2�Ҳ��һ�㣬������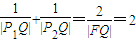 ��
��