摘要:(Ⅰ)证明:点的所有“相关弦 的中点的横坐标相同,
网址:http://m.1010jiajiao.com/timu_id_530544[举报]
(2009•崇明县二模)设椭圆C:
+
=1(a>b>0)的一个顶点坐标为A(0,-
),且其右焦点到直线y-x-2
=0的距离为3.
(1)求椭圆C的轨迹方程;
(2)若A、B是椭圆C上的不同两点,弦AB(不平行于y轴)的垂直平分线与x轴相交于点M,则称弦AB是点M的一条“相关弦”,如果点M的坐标为M(
,0),求证:点M的所有“相关弦”的中点在同一条直线上;
(3)对于问题(2),如果点M坐标为M(t,0),当t满足什么条件时,点M(t,0)存在无穷多条“相关弦”,并判断点M的所有“相关弦”的中点是否在同一条直线上.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
(1)求椭圆C的轨迹方程;
(2)若A、B是椭圆C上的不同两点,弦AB(不平行于y轴)的垂直平分线与x轴相交于点M,则称弦AB是点M的一条“相关弦”,如果点M的坐标为M(
| 1 |
| 2 |
(3)对于问题(2),如果点M坐标为M(t,0),当t满足什么条件时,点M(t,0)存在无穷多条“相关弦”,并判断点M的所有“相关弦”的中点是否在同一条直线上.
(2009•崇明县二模)设椭圆C:
+
=1(a>b>0)的一个顶点坐标为A(0,-
),且其右焦点到直线y-x-2
=0的距离为3.
(1)求椭圆C的轨迹方程;
(2)若A、B是椭圆C上的不同两点,弦AB(不平行于y轴)的垂直平分线与x轴相交于点M,则称弦AB是点M的一条“相关弦”,如果点M的坐标为M(
,0),求证点M的所有“相关弦”的中点在同一条直线上;
(3)根据解决问题(2)的经验与体会,请运用类比、推广等思想方法,提出一个与“相关弦”有关的具有研究价值的结论,并加以解决.(本小题将根据所提出问题的层次性给予不同的分值)
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
(1)求椭圆C的轨迹方程;
(2)若A、B是椭圆C上的不同两点,弦AB(不平行于y轴)的垂直平分线与x轴相交于点M,则称弦AB是点M的一条“相关弦”,如果点M的坐标为M(
| 1 |
| 2 |
(3)根据解决问题(2)的经验与体会,请运用类比、推广等思想方法,提出一个与“相关弦”有关的具有研究价值的结论,并加以解决.(本小题将根据所提出问题的层次性给予不同的分值)
(理)设斜率为k1的直线L交椭圆C: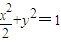 于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).
于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).
(1)求k1?k2的值.
(2)把上述椭圆C一般化为
(a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线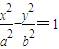 (a>0,b>0)中相类似的结论,并证明你的结论.
(a>0,b>0)中相类似的结论,并证明你的结论.
(3)分析(2)中的探究结果,并作出进一步概括,使上述结果都是你所概括命题的特例.
如果概括后的命题中的直线L过原点,P为概括后命题中曲线上一动点,借助直线L及动点P,请你提出一个有意义的数学问题,并予以解决.
查看习题详情和答案>>
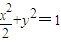 于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).
于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).(1)求k1?k2的值.
(2)把上述椭圆C一般化为

(a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线
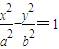 (a>0,b>0)中相类似的结论,并证明你的结论.
(a>0,b>0)中相类似的结论,并证明你的结论.(3)分析(2)中的探究结果,并作出进一步概括,使上述结果都是你所概括命题的特例.
如果概括后的命题中的直线L过原点,P为概括后命题中曲线上一动点,借助直线L及动点P,请你提出一个有意义的数学问题,并予以解决.
查看习题详情和答案>>
(理)设斜率为k1的直线L交椭圆C:
+y2=1于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).
(1)求k1?k2的值.
(2)把上述椭圆C一般化为
+
=1
(a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线
-
=1(a>0,b>0)中相类似的结论,并证明你的结论.
(3)分析(2)中的探究结果,并作出进一步概括,使上述结果都是你所概括命题的特例.
如果概括后的命题中的直线L过原点,P为概括后命题中曲线上一动点,借助直线L及动点P,请你提出一个有意义的数学问题,并予以解决.
查看习题详情和答案>>
| x2 |
| 2 |
(1)求k1?k2的值.
(2)把上述椭圆C一般化为
| x2 |
| a2 |
| y2 |
| b2 |
(a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线
| x2 |
| a2 |
| y2 |
| b2 |
(3)分析(2)中的探究结果,并作出进一步概括,使上述结果都是你所概括命题的特例.
如果概括后的命题中的直线L过原点,P为概括后命题中曲线上一动点,借助直线L及动点P,请你提出一个有意义的数学问题,并予以解决.
(2007•杨浦区二模)(理)设斜率为k1的直线L交椭圆C:
+y2=1于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).
(1)求k1?k2的值.
(2)把上述椭圆C一般化为
+
=1
(a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线
-
=1(a>0,b>0)中相类似的结论,并证明你的结论.
(3)分析(2)中的探究结果,并作出进一步概括,使上述结果都是你所概括命题的特例.
如果概括后的命题中的直线L过原点,P为概括后命题中曲线上一动点,借助直线L及动点P,请你提出一个有意义的数学问题,并予以解决.
查看习题详情和答案>>
| x2 |
| 2 |
(1)求k1?k2的值.
(2)把上述椭圆C一般化为
| x2 |
| a2 |
| y2 |
| b2 |
(a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线
| x2 |
| a2 |
| y2 |
| b2 |
(3)分析(2)中的探究结果,并作出进一步概括,使上述结果都是你所概括命题的特例.
如果概括后的命题中的直线L过原点,P为概括后命题中曲线上一动点,借助直线L及动点P,请你提出一个有意义的数学问题,并予以解决.