题目内容
(理)设斜率为k1的直线L交椭圆C: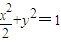 于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).
于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).(1)求k1?k2的值.
(2)把上述椭圆C一般化为

(a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线
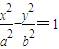 (a>0,b>0)中相类似的结论,并证明你的结论.
(a>0,b>0)中相类似的结论,并证明你的结论.(3)分析(2)中的探究结果,并作出进一步概括,使上述结果都是你所概括命题的特例.
如果概括后的命题中的直线L过原点,P为概括后命题中曲线上一动点,借助直线L及动点P,请你提出一个有意义的数学问题,并予以解决.
【答案】分析:(1)设直线方程为y=k1x+b,代入椭圆方程,根据方程的根与系数关系求弦中点M的坐标为 ,代入可得
,代入可得 ,从而可求
,从而可求
(法二)(利用点差法)设点A(x1,y1),B(x2,y2),中点M(x,y),由 与
与 作差得
作差得  =
=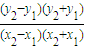 可求
可求
(2)已知斜率为K1的直线L交双曲线 (a>0,b>0)于A,B两点,点M 为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设K1、k2都存在).
(a>0,b>0)于A,B两点,点M 为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设K1、k2都存在).
则k1,k2?的值为
(解一)设直线方程为y=k1x+d,代入 ((a>0,b>0)方程并整,根据方程的根与系数的关系代入可求
((a>0,b>0)方程并整,根据方程的根与系数的关系代入可求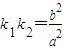
(解二)设点A(x1,y1),B(x2,y2),中点中点M(x,y)由点A,B在双曲线上,则利用点差法可求
(3)对(2)的概括:设斜率为k1的直线L交二次曲线C:mx2+ny2=1(mn≠0)于A,B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1,k2、都存在),则 .
.
解答:(解一):(1)设直线方程为y=k1x+b,代入椭圆方程并整理得:(1+2k12)x2+4k1bx+2b2-2=0,(2分)
 ,又中点M在直线上,所以
,又中点M在直线上,所以
从而可得弦中点M的坐标为 ,
, ,所以
,所以 .(4分)
.(4分)
(解二)设点A(x1,y1),B(x2,y2),中点M(x,y) 则 ,
,
 =
= ,
, (2分)
(2分)
又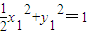 与
与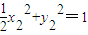 作差得
作差得 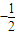 =
=
所以 (4分)
(4分)
(2)对于椭圆, (6分)
(6分)
已知斜率为K1的直线L交双曲线 (a>0,b>0)于A,B两点,点M 为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设K1、k2都存在).
(a>0,b>0)于A,B两点,点M 为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设K1、k2都存在).
则k1,k2?的值为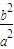 . (8分)
. (8分)
(解一)设直线方程为y=k1x+d,代入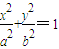 ((a>0,b>0)方程并整理得:(b2-a2k12)x2-2k1a2dx-(ad)2-(ab)2=0
((a>0,b>0)方程并整理得:(b2-a2k12)x2-2k1a2dx-(ad)2-(ab)2=0
 ,
,
所以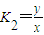 =
= =
=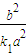 ,
, (2分),即
(2分),即 (10分)
(10分)
(解二)设点A(x1,y1),B(x2,y2),中点中点M(x,y)
则 ,
, ,
,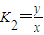 =
= ,
, (2分)
(2分)
又因为点A,B在双曲线上,则
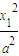
 与
与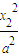
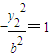 作差得
作差得
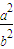 =
= =k1k2 即
=k1k2 即 (10分)
(10分)
(3)对(2)的概括:设斜率为k1的直线L交二次曲线C:mx2+ny2=1(mn≠0)于A,B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1,k2、都存在),则 .(12分)
.(12分)
提出问题与解决问题满分分别为(3分),提出意义不大的问题不得分,解决问题的分值不得超过提出问题的分值.
提出的问题例如:直线L过原点,P为二次曲线线mx2+ny2=1(mn≠0)上一动点,设直线L交曲线于A,B两点,当P异于A,B两点时,如果直线PA,PB的斜率都存在,则它们斜率的积为与点P无关的定值.(15分)
解法1:设直线方程为y=kx,A,B两点坐标分别为(x1,y1)、(-x1,-y1),则y1=kx1
把y=kx代入mx2+ny2=1得(m+nk2)x2=1,
KPA•KPB=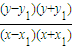 =
=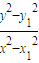 ,
,
所以KPA•KPB= =
=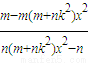 =
= (18分)
(18分)
提出的问题的例如:直线L:y=x,P为二次曲线mx2+ny2=1(mn≠0)上一动点,设直线L交曲线于A,B两点.试问使∠APB=30°的点P是否存在?(13分)
问题例如:1)直线L过原点,P为二次曲线线mx2+ny2=1(mn≠0)上一动点,设直线L交曲线于A,B两点,求PA+PB的值.
2)直线l过原点,P为二次曲线mx2+ny2=1(mn≠0)上一动点,设直线L交曲线于A,B两点,求S△PAB的最值.
点评:本题主要考查了直线与曲线的相交关系的应用,解题的关键是能够由椭圆的性质归纳推理 到一般的曲线方程,及较强的逻辑推理的运算能力
 ,代入可得
,代入可得 ,从而可求
,从而可求(法二)(利用点差法)设点A(x1,y1),B(x2,y2),中点M(x,y),由
 与
与 作差得
作差得  =
=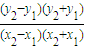 可求
可求(2)已知斜率为K1的直线L交双曲线
 (a>0,b>0)于A,B两点,点M 为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设K1、k2都存在).
(a>0,b>0)于A,B两点,点M 为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设K1、k2都存在).则k1,k2?的值为

(解一)设直线方程为y=k1x+d,代入
 ((a>0,b>0)方程并整,根据方程的根与系数的关系代入可求
((a>0,b>0)方程并整,根据方程的根与系数的关系代入可求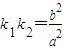
(解二)设点A(x1,y1),B(x2,y2),中点中点M(x,y)由点A,B在双曲线上,则利用点差法可求
(3)对(2)的概括:设斜率为k1的直线L交二次曲线C:mx2+ny2=1(mn≠0)于A,B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1,k2、都存在),则
 .
.解答:(解一):(1)设直线方程为y=k1x+b,代入椭圆方程并整理得:(1+2k12)x2+4k1bx+2b2-2=0,(2分)
 ,又中点M在直线上,所以
,又中点M在直线上,所以
从而可得弦中点M的坐标为
 ,
, ,所以
,所以 .(4分)
.(4分)(解二)设点A(x1,y1),B(x2,y2),中点M(x,y) 则
 ,
,
 =
= ,
, (2分)
(2分)又
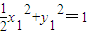 与
与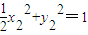 作差得
作差得 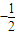 =
=
所以
 (4分)
(4分)(2)对于椭圆,
 (6分)
(6分)已知斜率为K1的直线L交双曲线
 (a>0,b>0)于A,B两点,点M 为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设K1、k2都存在).
(a>0,b>0)于A,B两点,点M 为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设K1、k2都存在).则k1,k2?的值为
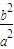 . (8分)
. (8分)(解一)设直线方程为y=k1x+d,代入
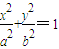 ((a>0,b>0)方程并整理得:(b2-a2k12)x2-2k1a2dx-(ad)2-(ab)2=0
((a>0,b>0)方程并整理得:(b2-a2k12)x2-2k1a2dx-(ad)2-(ab)2=0 ,
,所以
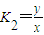 =
= =
=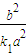 ,
, (2分),即
(2分),即 (10分)
(10分)(解二)设点A(x1,y1),B(x2,y2),中点中点M(x,y)
则
 ,
, ,
,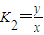 =
= ,
, (2分)
(2分)又因为点A,B在双曲线上,则
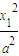
 与
与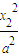
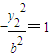 作差得
作差得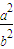 =
= =k1k2 即
=k1k2 即 (10分)
(10分)(3)对(2)的概括:设斜率为k1的直线L交二次曲线C:mx2+ny2=1(mn≠0)于A,B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1,k2、都存在),则
 .(12分)
.(12分)提出问题与解决问题满分分别为(3分),提出意义不大的问题不得分,解决问题的分值不得超过提出问题的分值.
提出的问题例如:直线L过原点,P为二次曲线线mx2+ny2=1(mn≠0)上一动点,设直线L交曲线于A,B两点,当P异于A,B两点时,如果直线PA,PB的斜率都存在,则它们斜率的积为与点P无关的定值.(15分)
解法1:设直线方程为y=kx,A,B两点坐标分别为(x1,y1)、(-x1,-y1),则y1=kx1
把y=kx代入mx2+ny2=1得(m+nk2)x2=1,
KPA•KPB=
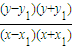 =
=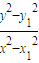 ,
,所以KPA•KPB=
 =
=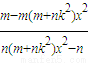 =
= (18分)
(18分)提出的问题的例如:直线L:y=x,P为二次曲线mx2+ny2=1(mn≠0)上一动点,设直线L交曲线于A,B两点.试问使∠APB=30°的点P是否存在?(13分)
问题例如:1)直线L过原点,P为二次曲线线mx2+ny2=1(mn≠0)上一动点,设直线L交曲线于A,B两点,求PA+PB的值.
2)直线l过原点,P为二次曲线mx2+ny2=1(mn≠0)上一动点,设直线L交曲线于A,B两点,求S△PAB的最值.
点评:本题主要考查了直线与曲线的相交关系的应用,解题的关键是能够由椭圆的性质归纳推理 到一般的曲线方程,及较强的逻辑推理的运算能力

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目