摘要：从而所求直线方程为．
网址：http://m.1010jiajiao.com/timu_id_530479[举报]
已知L为过点P
且倾斜角为30°的直线，圆C为圆心是坐标原点且半径等于1的圆，Q表示顶点在原点而焦点是
的抛物线，设A为L和C在第三象限的交点，B为C和Q在第四象限的交点．
（1）写出直线L、圆C和抛物线Q的方程，并作草图．
（2）写出线段PA、圆弧AB和抛物线上OB一段的函数表达式．
（3）设P′、B′依次为从P、B到x轴的垂足，求由圆弧AB和直线段BB′、B′P′、P′P、PA所包含的面积．
查看习题详情和答案>>
且倾斜角为30°的直线，圆C为圆心是坐标原点且半径等于1的圆，Q表示顶点在原点而焦点是的抛物线，设A为L和C在第三象限的交点，B为C和Q在第四象限的交点．（1）写出直线L、圆C和抛物线Q的方程，并作草图．
（2）写出线段PA、圆弧AB和抛物线上OB一段的函数表达式．
（3）设P′、B′依次为从P、B到x轴的垂足，求由圆弧AB和直线段BB′、B′P′、P′P、PA所包含的面积．
查看习题详情和答案>>
已知L为过点P(-
，-
)且倾斜角为30°的直线，圆C为圆心是坐标原点且半径等于1的圆，Q表示顶点在原点而焦点是(
，0)的抛物线，设A为L和C在第三象限的交点，B为C和Q在第四象限的交点．
（1）写出直线L、圆C和抛物线Q的方程，并作草图．
（2）写出线段PA、圆弧AB和抛物线上OB一段的函数表达式．
（3）设P′、B′依次为从P、B到x轴的垂足，求由圆弧AB和直线段BB′、B′P′、P′P、PA所包含的面积． 查看习题详情和答案>>
3
| ||
| 2 |
| 3 |
| 2 |
| ||
| 8 |
（1）写出直线L、圆C和抛物线Q的方程，并作草图．
（2）写出线段PA、圆弧AB和抛物线上OB一段的函数表达式．
（3）设P′、B′依次为从P、B到x轴的垂足，求由圆弧AB和直线段BB′、B′P′、P′P、PA所包含的面积． 查看习题详情和答案>>
已知点A(0，2)和圆C：(x－6)2＋(y－4)2＝
，一条光线从A点出发射到x轴上后沿圆的切线方向反射，求这条光线从A点到切点所经过的路程．
思路分析：先画出示意图，再利用对称性求解问题．类似这种关于光的反射问题，通常都利用对称性作出题中图形对“镜面”的对称图形，从而化折线问题为直线问题．
为了了解某地母亲身高x与女儿身高y的相关关系，随机测得10对母女的身高如下表所示：
计算x与y的相关系数r=0.71，通过查表得r的临界值r0.05= ，从而有 的把握认为x与y之间具有线性相关关系，因而求回归直线方程是有意义的．通过计算得到回归直线方程为y=35.2+0.78x，当母亲身高每增加1cm时，女儿身高 ，当母亲的身高为161cm时，估计女儿的身高为 cm．
查看习题详情和答案>>
| 母亲身高x（cm） | 159 | 160 | 160 | 163 | 159 | 154 | 159 | 158 | 159 | 157 |
| 女儿身高y（cm） | 158 | 159 | 160 | 161 | 161 | 155 | 162 | 157 | 162 | 156 |
为了了解某地母亲身高x与女儿身高Y的相关关系，随机测得10对母女的身高如下表所示：
计算x与Y的相关系数r≈0.71，通过查表得r的临界值r0.05=0.632，从而有 的把握认为x与Y之间具有线性相关关系，因而求回归直线方程是有意义的．通过计算得到回归直线方程为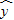
═34.92+0.78x，因此，当母亲的身高为161cm时，可以估计女儿的身高大致为 ．
查看习题详情和答案>>
| 母亲身x（cm） | 159 | 160 | 160 | 163 | 159 | 154 | 159 | 158 | 159 | 157 |
| 女儿身Y（cm） | 158 | 159 | 160 | 161 | 161 | 155 | 162 | 157 | 162 | 156 |
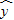═34.92+0.78x，因此，当母亲的身高为161cm时，可以估计女儿的身高大致为 ．
查看习题详情和答案>>