题目内容
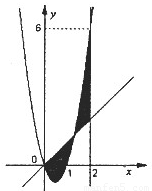
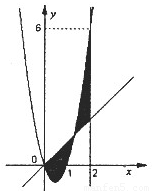
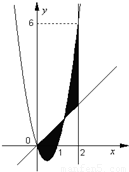
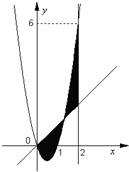 如图,已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=3tx(其中-1<t<1,t为数);.若直线l2与函数f(x)的图象以及直线l1,l2与函数f(x)的图象所围成的封闭图形如阴影所示.
如图,已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=3tx(其中-1<t<1,t为数);.若直线l2与函数f(x)的图象以及直线l1,l2与函数f(x)的图象所围成的封闭图形如阴影所示.(1)求y=f(x);
(2)求阴影面积s关于t的函数y=s(t)的解析式;(3)若过点A(1,m),m≠4可作曲线y=s(t),t∈R的三条切线,求实数m的取值范围.
分析:(1)由图象观察得到二次函数f(x)过点(0,0),(1,0),就可设出二次函数的两根式,再由图象观察得到二次函数图象还过点(2,6),代入两根式,就可求出函数f(x)的解析式.
(2)先求出二次函数与直线l2的交点横坐标,分别为0,1+t,由定积分的几何意义可知,阴影部分的面积分成两部分,左边部分是函数y=3tx与函数y=3x2-3x的差在积分区间[0,1+t]上的定积分,右边部分是函数y=3x2-3x与函数y=3tx的差在积分区间[1+t,2]上的定积分,分别求出,再相加即可.
(3)先判断点A(1,m)在不在曲线s(t)上,因为曲线的切线斜率是曲线在切点处的导数,若过点A(1,m)可作曲线的三条切线,则曲线在切点处的导数满足3(1+x0)2-6=
有三个实根,再利用导数判断m为何值时关于x0方程2x03-6x0+m=0有三个实根即可.
(2)先求出二次函数与直线l2的交点横坐标,分别为0,1+t,由定积分的几何意义可知,阴影部分的面积分成两部分,左边部分是函数y=3tx与函数y=3x2-3x的差在积分区间[0,1+t]上的定积分,右边部分是函数y=3x2-3x与函数y=3tx的差在积分区间[1+t,2]上的定积分,分别求出,再相加即可.
(3)先判断点A(1,m)在不在曲线s(t)上,因为曲线的切线斜率是曲线在切点处的导数,若过点A(1,m)可作曲线的三条切线,则曲线在切点处的导数满足3(1+x0)2-6=
| (1+x0)3-6x0+2-m |
| x0-1 |
解答: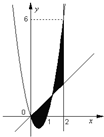 解:(1)由图可知二次函数的图象过点(0,0),(1,0)
解:(1)由图可知二次函数的图象过点(0,0),(1,0)
则f(x)=ax(x-1),
又因为图象过点(2,6)
∴6=2a∴a=3
∴函数f(x)的解析式为f(x)=3x(x-1)=3x2-3x
(2)由
得x2-(1+t)x=0,∴x1=0,x2=1+t,
∵-1<t<1,∴直线l2与f(x)的图象的交点横坐标分别为0,1+t,
由定积分的几何意义知:s(t)=
[3tx-(3x2-3x)]dx+
[(3x2-3x)-3tx]dx
=(
x2 -x3)
+(
x2 +x3)
=(1+t)3+2-6t,(-1<t<1);
(3)∵曲线方程为s(t)=(1+t)3+2-6t,t∈R,∴s'(t)=3(1+t)2-6,
∴点A(1,m),m≠4不在曲线上.
设切点为M(x0,y0),则点M的坐标满足y0=(1+x0)3+2-6x0,
∵s'(x0)=3(1+x0)2-6,故切线的斜率为3(1+x0)2-6=
=
,
整理得2x03-6x0+m=0.
∵过点A(1,m)可作曲线的三条切线,∴关于x0方程2x03-6x0+m=0有三个实根.
设g(x0)=2x03-6x0+m,则g'(x0)=6x02-6,由g'(x0)=0得x0=±1
∵当x0∈(-∞,-1)∪(1,+∞)时,g'(x0)>0∴g(x0)在(-∞,-1),(1,+∞)上单调递增,
∵当x0∈(-1,1)时,g'(x0)<0,∴g(x0)在(-1,1)上单调递减.
∴函数g(x0)=2x03-6x0+m的极值点为x0=±1,
∴关于x0方程2x03-6x0+m=0有三个实根的充要条件是
,即
解得-4<m<4,
故所求的实数m的取值范围是-4<m<4.
 解:(1)由图可知二次函数的图象过点(0,0),(1,0)
解:(1)由图可知二次函数的图象过点(0,0),(1,0)则f(x)=ax(x-1),
又因为图象过点(2,6)
∴6=2a∴a=3
∴函数f(x)的解析式为f(x)=3x(x-1)=3x2-3x
(2)由
|
∵-1<t<1,∴直线l2与f(x)的图象的交点横坐标分别为0,1+t,
由定积分的几何意义知:s(t)=
| ∫ | 1+t 0 |
| ∫ | 2 1+t |
=(
| 3t+3 |
| 2 |
| | | 1+t 0 |
| -3t-3 |
| 2 |
| | | 2 1+t |
=(1+t)3+2-6t,(-1<t<1);
(3)∵曲线方程为s(t)=(1+t)3+2-6t,t∈R,∴s'(t)=3(1+t)2-6,
∴点A(1,m),m≠4不在曲线上.
设切点为M(x0,y0),则点M的坐标满足y0=(1+x0)3+2-6x0,
∵s'(x0)=3(1+x0)2-6,故切线的斜率为3(1+x0)2-6=
| y0-m |
| x0-1 |
| (1+x0)3-6x0+2-m |
| x0-1 |
整理得2x03-6x0+m=0.
∵过点A(1,m)可作曲线的三条切线,∴关于x0方程2x03-6x0+m=0有三个实根.
设g(x0)=2x03-6x0+m,则g'(x0)=6x02-6,由g'(x0)=0得x0=±1
∵当x0∈(-∞,-1)∪(1,+∞)时,g'(x0)>0∴g(x0)在(-∞,-1),(1,+∞)上单调递增,
∵当x0∈(-1,1)时,g'(x0)<0,∴g(x0)在(-1,1)上单调递减.
∴函数g(x0)=2x03-6x0+m的极值点为x0=±1,
∴关于x0方程2x03-6x0+m=0有三个实根的充要条件是
|
|
解得-4<m<4,
故所求的实数m的取值范围是-4<m<4.
点评:本题(1)考查了待定系数法求函数解析式,(2)考察了定积分在几何中的应用;(3)考查了导数的几何意义,导数与函数的单调区间,极值的关系,属于综合题.

练习册系列答案
相关题目
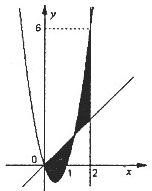 如图,已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=3tx(其中-1<t<1,t为常数);若直线l2与函数f(x)的图象以及直线l1,l2与函数f(x)以及的图象所围成的封闭图形如阴影所示.
如图,已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=3tx(其中-1<t<1,t为常数);若直线l2与函数f(x)的图象以及直线l1,l2与函数f(x)以及的图象所围成的封闭图形如阴影所示.