题目内容
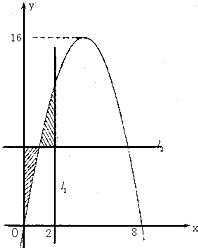 已知二次函数f(x)=ax2+bx+c,直线l1:y=-t2+8t(其中0≤t≤2.t为常数);l2:x=2.若直线l1、l2与函数f(x)的图象以及l1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示.
已知二次函数f(x)=ax2+bx+c,直线l1:y=-t2+8t(其中0≤t≤2.t为常数);l2:x=2.若直线l1、l2与函数f(x)的图象以及l1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示.(1)求a、b、c的值.
(2)求阴影面积S关于t的函数S(t)的解析式.
分析:(1)由图知(0,0)和(8,0)在函数图象上,以及f(x)的最大值为16,代入函数解析式和顶点的纵坐标,列出方程组求出a、b、c的值;
(2)由图知先求出联立直线l1与f(x)的方程,求出它们图象的交点坐标,再根据定积分的几何意义求出阴影部分的面积.
(2)由图知先求出联立直线l1与f(x)的方程,求出它们图象的交点坐标,再根据定积分的几何意义求出阴影部分的面积.
解答:解:(1)由图形可知二次函数的图象过点(0,0),(8,0),并且f(x)的最大值为16
则
解之得:
,
∴函数f(x)的解析式为f(x)=-x2+8x
(2)由
得x2-8x-t(t-8)=0,∴x1=t,x2=8-t,
∵0≤t≤2,∴直线l1与f(x)的图象的交点坐标为(t,-t2+8t)
由定积分的几何意义知:S(t)=
[(-t2+8t)-(-x2+8x)]dx+
[(-x2+8x)-(-t2+8t]dx
=[(-t2+8t)x-(-
+4x2)] |_t+[(-
+4x2)-(-t2+8t)•x]
=-
t3+10t2-16t+
.
则
|
|
∴函数f(x)的解析式为f(x)=-x2+8x
(2)由
|
∵0≤t≤2,∴直线l1与f(x)的图象的交点坐标为(t,-t2+8t)
由定积分的几何意义知:S(t)=
| ∫ | t 0 |
| ∫ | 2 t |
=[(-t2+8t)x-(-
| x3 |
| 3 |
| x3 |
| 3 |
| | | 2 t |
=-
| 4 |
| 3 |
| 40 |
| 3 |
点评:本题考查了由图象求函数的解析式和阴影部分的面积,即根据点在图象上则点的坐标满足方程求解析式,用定积分求面积时应先求出交点的坐标,考查了读图能力和数形结合思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目