题目内容
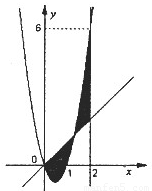
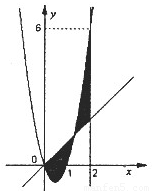
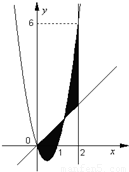
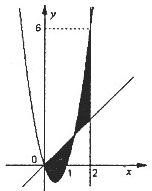 如图,已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=3tx(其中-1<t<1,t为常数);若直线l2与函数f(x)的图象以及直线l1,l2与函数f(x)以及的图象所围成的封闭图形如阴影所示.
如图,已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=3tx(其中-1<t<1,t为常数);若直线l2与函数f(x)的图象以及直线l1,l2与函数f(x)以及的图象所围成的封闭图形如阴影所示.(I)求y=f(x);
(2)求阴影面积s关于t的函数y=s(t)的解析式.
分析:(1)已知二次函数的解析式f(x)=ax2+bx+c过点(0,0),(1,0),(2,6)利用待定系数法求出a,b,c,从而求出f(x);
(2)直线l2:y=3tx与函数f(x)进行联立方程,求出交点,再利用定积分的集合意义及运算法则进行计算,求出阴影的面积;
(2)直线l2:y=3tx与函数f(x)进行联立方程,求出交点,再利用定积分的集合意义及运算法则进行计算,求出阴影的面积;
解答:解:(1)由图可知二次函数的图象过点(0,0),(1,0)
则f(x)=ax(x-1),
又因为图象过点(2,6)
∴6=2a
∴a=3
∴函数f(x)的解析式为f(x)=3x(x-1)=3x2-3x
(2)由
得x2-(1+t)x=0,
∴x1=0,x2=1+t,
∵-1<t<1,
∴直线l2与f(x)的图象的交点横坐标分别为0,1+t,
由定积分的几何意义知:s(t)
[3tx-(3x2-3x)]dx
[(3x2-3x)-3tx]dx
=[
x2-x3]
+[x3-
x2]
=(1+t)3+2-6t,(-1<t<1);
则f(x)=ax(x-1),
又因为图象过点(2,6)
∴6=2a
∴a=3
∴函数f(x)的解析式为f(x)=3x(x-1)=3x2-3x
(2)由
|
∴x1=0,x2=1+t,
∵-1<t<1,
∴直线l2与f(x)的图象的交点横坐标分别为0,1+t,
由定积分的几何意义知:s(t)
| =∫ | 1+t 0 |
| +∫ | 2 1+t |
=[
| 3(1+t) |
| 2 |
| | | t+1 0 |
| 3(1+t) |
| 2 |
| | | 2 t+1 |
点评:此题主要考查定积分的应用,考查的知识点比较全面,有一定的难度,第二问计算量比较大,是一到中档题;

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
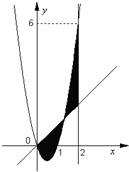 如图,已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=3tx(其中-1<t<1,t为数);.若直线l2与函数f(x)的图象以及直线l1,l2与函数f(x)的图象所围成的封闭图形如阴影所示.
如图,已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=3tx(其中-1<t<1,t为数);.若直线l2与函数f(x)的图象以及直线l1,l2与函数f(x)的图象所围成的封闭图形如阴影所示.