摘要：知.
网址：http://m.1010jiajiao.com/timu_id_516692[举报]
（I） 已知抛物线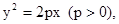
过焦点
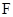的动直线l交抛物线于A，B两点，O为坐标原点, 求证: 
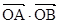为定值;
（Ⅱ）由 （Ⅰ） 可知: 过抛物线的焦点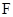的动直线 l 交抛物线于
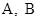两点, 存在定点
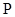, 使得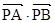
为定值. 请写出关于椭圆的类似结论,并给出证明.
（I） 已知抛物线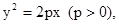
过焦点
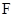的动直线l交抛物线于A，B两点，O为坐标原点, 求证: 
为定值;
（Ⅱ）由 （Ⅰ） 可知: 过抛物线的焦点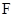的动直线 l 交抛物线于
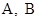两点, 存在定点
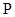, 使得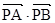
为定值. 请写出关于椭圆的类似结论,并给出证明.
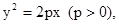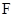过焦点的动直线l交抛物线于A，B两点，O为坐标原点, 求证: 为定值;（Ⅱ）由 （Ⅰ） 可知: 过抛物线的焦点
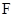的动直线 l 交抛物线于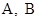两点, 存在定点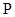, 使得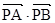为定值. 请写出关于椭圆的类似结论,并给出证明.
（1）选修4-2：矩阵与变换
已知矩阵M=（
）的两^E值分别为λ1=-1和λ2=4．
（I）求实数的值；
（II ）求直线x-2y-3=0在矩阵M所对应的线性变换作用下的像的方程．
（2）选修4-4：坐标系与参数方程
在直角坐标平面内，以坐标原点O为极点x轴的非负半轴为极轴建立极坐标系．已知曲线C的参数方程为
，
（a为餓），曲线D的鍵标方程为ρsin（θ-
）=-
．
（I ）将曲线C的参数方程化为普通方程；
（II）判断曲线c与曲线D的交点个数，并说明理由．
（3）选修4-5：不等式选讲
已知a，b为正实数．
（I）求证：
+
≥a+b；
（II）利用（I）的结论求函数y=
+
（0＜x＜1）的最小值．
查看习题详情和答案>>
已知矩阵M=（
|
（I）求实数的值；
（II ）求直线x-2y-3=0在矩阵M所对应的线性变换作用下的像的方程．
（2）选修4-4：坐标系与参数方程
在直角坐标平面内，以坐标原点O为极点x轴的非负半轴为极轴建立极坐标系．已知曲线C的参数方程为
|
（a为餓），曲线D的鍵标方程为ρsin（θ-
| π |
| 4 |
3
| ||
| 2 |
（I ）将曲线C的参数方程化为普通方程；
（II）判断曲线c与曲线D的交点个数，并说明理由．
（3）选修4-5：不等式选讲
已知a，b为正实数．
（I）求证：
| a2 |
| b |
| b2 |
| a |
（II）利用（I）的结论求函数y=
| (1-x)2 |
| x |
| x2 |
| 1-x |
（1）已知
=（2x-y+1，x+y-2），
=（2，-2），①当x、y为何值时，
与
共线？②是否存在实数x、y，使得
⊥
，且|
|=|
|？若存在，求出xy的值；若不存在，说明理由．
（2）设
和
是两个单位向量，其夹角是90°，
=
+2
，
=-3
+
，若(k
-
)⊥(
+k
)，求实数k的值．
查看习题详情和答案>>
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
（2）设
| i |
| j |
| a |
| i |
| j |
| b |
| i |
| j |
| a |
| b |
| a |
| b |
（1）选修4-4：矩阵与变换
已知曲线C1：y=
绕原点逆时针旋转45°后可得到曲线C2：y2-x2=2，
（I）求由曲线C1变换到曲线C2对应的矩阵M1；
（II）若矩阵M2=
，求曲线C1依次经过矩阵M1，M2对应的变换T1，T2变换后得到的曲线方程．
（2）选修4-4：坐标系与参数方程
已知直线l的极坐标方程是ρcosθ+ρsinθ-1=0．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，在曲线C：
（θ为参数）上求一点，使它到直线l的距离最小，并求出该点坐标和最小距离．
（3）（选修4-5：不等式选讲）
将12cm长的细铁线截成三条长度分别为a、b、c的线段，
（I）求以a、b、c为长、宽、高的长方体的体积的最大值；
（II）若这三条线段分别围成三个正三角形，求这三个正三角形面积和的最小值．
查看习题详情和答案>>
已知曲线C1：y=
| 1 |
| x |
（I）求由曲线C1变换到曲线C2对应的矩阵M1；
（II）若矩阵M2=
|
（2）选修4-4：坐标系与参数方程
已知直线l的极坐标方程是ρcosθ+ρsinθ-1=0．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，在曲线C：
|
（3）（选修4-5：不等式选讲）
将12cm长的细铁线截成三条长度分别为a、b、c的线段，
（I）求以a、b、c为长、宽、高的长方体的体积的最大值；
（II）若这三条线段分别围成三个正三角形，求这三个正三角形面积和的最小值．