网址:http://m.1010jiajiao.com/timu_id_502270[举报]
一、选择题BBCAA BBAAD
11、-6 12、 13、4
13、4  14、
14、 15、
15、
16.解:(1)在 中,由
中,由 ,得
,得 ……………………2分
……………………2分
又由正弦定理 ………3分 得:
………3分 得: ………………4分
………………4分
(2)由余弦定理: 得:
得: ……6分
……6分
即 ,解得
,解得 或
或 (舍去),所以
(舍去),所以 ………………8分
………………8分
所以,
 ……………10分
……………10分
 ,即
,即 …………………… ……… ……12分
…………………… ……… ……12分


18、(本小题满分14分)
(1)连接BD,由已知有
得 ………………………………(1分)
………………………………(1分)
又由ABCD是正方形,得: …(2分)
…(2分)
∵ 与BD相交,∴
与BD相交,∴ …………………………(3分)
…………………………(3分)
(2)延长DC至G,使CG=EB,,连结BG、D
 ,∴四边形EBGC是平行四边形.
,∴四边形EBGC是平行四边形.
∴BG∥EC. ∴ 就是异面直线BD1与CE所成角…………………………(5分)
就是异面直线BD1与CE所成角…………………………(5分)
在 中,
中,
 …………………(6分)
…………………(6分)


 异面直线
异面直线  与CE所成角的余弦值是
与CE所成角的余弦值是 ……………………………(8分)
……………………………(8分)
(3)∵ ∴
∴
又∵ ∴ 点E到
∴ 点E到 的距离
的距离 ……………(9分)
……………(9分)
有:
 , ………………(11分)
, ………………(11分)
又由 ,
设点B到平面
,
设点B到平面 的距离为
的距离为 ,
,
则:
有: …………………………………(13分)
…………………………………(13分)
 所以:点B到平面
所以:点B到平面 的距离为
的距离为 。……………(14分)
。……………(14分)
19.解:(1)由题意可知当
 ……3分
……3分
每件产品的销售价格为 ……………………………4分
……………………………4分
∴2009年的利润 
 ………………… 7分
………………… 7分
(2) ,……………………………11分
,……………………………11分
 (万元)13分
(万元)13分
答:(略)…………………………………………………………………… 14分
20、解:(Ⅰ)圆 , 半径
, 半径

 QM是P的中垂线,连结AQ,则|AQ|=|QP|
QM是P的中垂线,连结AQ,则|AQ|=|QP|
 又
又 ,
,
根据椭圆的定义,点Q轨迹是以C(- ,0),A(
,0),A( ,0)为焦点,长轴长为2
,0)为焦点,长轴长为2 的
的
椭圆,………2分
由 因此点Q的轨迹方程为
因此点Q的轨迹方程为 ………………4分
………………4分
(Ⅱ)(1)证明:当直线l垂直x轴时,由题意知:
不妨取 代入曲线E的方程得:
代入曲线E的方程得: 
即G( ,
, ),H(
),H( ,-
,- )有两个不同的交点,………………5分
)有两个不同的交点,………………5分
当直线l不垂直x轴时,设直线l的方程为:
由题意知:
由

∴直线l与椭圆E交于两点, 综上,直线l必与椭圆E交于两点…………8分
(2)由(1)知当直线l垂直x轴时,
 ………………9分
………………9分
当直线l不垂直x轴时
设 (1)知
(1)知 



 …………………………10分
…………………………10分

当且仅当 ,则取得“=”
,则取得“=”
 ……………………12分
……………………12分
当k=0时, 综上,△OGH的面积的最小值为
综上,△OGH的面积的最小值为 …14分
…14分
21.解:(1)在已知式中,当 时,
时,
∵ ∴
∴ …………2分
…………2分
当 时,
时, ①
①  ②
②
①-②得,
∵ ∴
∴ =
= ③
③
∵ 适合上式…………4分 当
适合上式…………4分 当 时,
时,  ④
④
③-④得: 
∵ ∴
∴ ∴数列
∴数列 是等差数列,首项为1,公差为1,可得
是等差数列,首项为1,公差为1,可得
(2)假设存在整数 ,使得对任意
,使得对任意  ,都有
,都有 .
.
∵ ∴
∴
∴

∴ ⑤……………………………………………8分
⑤……………………………………………8分
当 (
( )时,⑤式即为
)时,⑤式即为 ⑥
⑥
依题意,⑥式对 都成立,∴λ<1……………………………………10分
都成立,∴λ<1……………………………………10分
当 (
( )时,⑤式即为
)时,⑤式即为 ⑦
⑦
依题意,⑦式对 都成立, ∴
都成立, ∴ ……………12分
……………12分
∴ ∴存在整数
∴存在整数 ,使得对任意
,使得对任意 ,都有
,都有 …14分
…14分
关于某设备的使用年限
x(年)和所支出的维修费用y(万元)有如下统计资料:
若由资料知,
y对x呈线性相关关系,试求:(1)
回归直线方程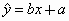 的回归系数b与a;
的回归系数b与a;
(2)
估计使用年限为10年时,维修费用约是多少? 查看习题详情和答案>>| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
(参考:b=
| |||||||
|
. |
| y |
. |
| x |
| 2 | 3 | 4 | 5 | 6 | |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,求出y关于x的线性回归方程y=
 |
| b |
 |
| a |
(Ⅲ)估计使用年限为10年时,维修费用约是多少?
(参考数据:2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3) 查看习题详情和答案>>
