摘要：BC平面A′BC ∴平面A′BC⊥平面A′EC ----------------9分(3)证明:在△A′EC中.P为A′C的中点.∴EP⊥A′C. 在△A′AC中.EP∥A′A.∴A′A⊥A′C
网址：http://m.1010jiajiao.com/timu_id_496775[举报]
如图，在四棱锥S-ABCD中，AD∥BC且AD⊥CD；平面CSD⊥平面ABCD，CS⊥DS，CS=2AD=2；E为BS的中点，CE=| 2 |
| 3 |
（Ⅰ）点A到平面BCS的距离；
（Ⅱ）二面角E-CD-A的大小． 查看习题详情和答案>>
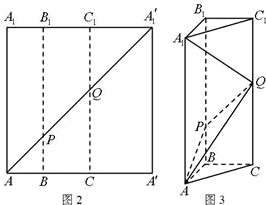如图2所示，在边长为12的正方形AA'A'1A1中，点B，C在线段AA'上，且AB=3，BC=4，作BB1∥AA1，分别交A1A'1、AA'1于点B1、P，作CC1∥AA1，分别交A1A'1、AA'1于点C1、Q，将该正方形沿BB1、CC1折叠，使得A'A1′与AA1重合，构成如图3所示的三棱柱ABC-A1B1C1．（1）在三棱柱ABC-A1B1C1中，求证：AB⊥平面BCC1B1．
（2）求平面APQ将三棱柱ABC-A1B1C1分成上、下两部分几何体的体积之比．
（3）在三棱柱ABC-A1B1C1中，求直线AP与直线A1Q所成角的余弦值． 查看习题详情和答案>>
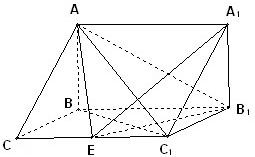如图，在三棱拄ABC-A1B1C1中，AB⊥侧面BB1C1C，已知BC=1，BB1=C1C，∠BCC1=