题目内容
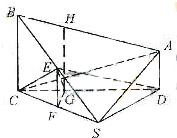
 如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=
如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=| 2 |
| 3 |
(Ⅰ)点A到平面BCS的距离;
(Ⅱ)二面角E-CD-A的大小.
分析:(Ⅰ)根据线面平行的判定定理可知AD∥平面BCS,则从而A点到平面BCS的距离等于D点到平面BCS的距离,从而DS为点A到平面BCS的距离,在Rt△ADS中求出DS即可;
(Ⅱ)过E点作EG⊥CD,交CD于点G,又过G点作GH⊥CD,交AB于H,根据二面角平面角的定义可知∠EGH为二面角E-CD-A的平面角,过E点作EF∥BC,交CS于点F,连接GF,在Rt△FEG中,求出此角即可.
(Ⅱ)过E点作EG⊥CD,交CD于点G,又过G点作GH⊥CD,交AB于H,根据二面角平面角的定义可知∠EGH为二面角E-CD-A的平面角,过E点作EF∥BC,交CS于点F,连接GF,在Rt△FEG中,求出此角即可.
解答:解:(Ⅰ)因为AD∥BC,且BC?平面BCS,
所以AD∥平面BCS,
从而A点到平面BCS的距离等于D点到平面BCS的距离.
因为平面CSD⊥平面ABCD,AD⊥CD,
故AD⊥平面CSD,从而AD⊥SD,
由AD∥BC,得BC⊥DS,又由CS⊥DS知DS⊥平面BCS,
从而DS为点A到平面BCS的距离,
因此在Rt△ADS中DS=
=
=
 (Ⅱ)如图,过E电作EG⊥CD,交CD于点G,
(Ⅱ)如图,过E电作EG⊥CD,交CD于点G,
又过G点作GH⊥CD,交AB于H,
故∠EGH为二面角E-CD-A的平面角,
记为θ,过E点作EF∥BC,交CS于点F,连接GF,
因平面ABCD⊥平面CSD,GH⊥CD,
易知GH⊥GF,故θ=
-∠EGF.
由于E为BS边中点,故CF=
CS=1,
在Rt△CFE中,EF=
=
=1,
因EF⊥平面CSD,又EG⊥CD
故由三垂线定理的逆定理得FG⊥CD,
从而又可得△CGF~△CSD,
因此
=
而在Rt△CSD中,
CD=
=
=
,
故GF=
•DS=
•
=
在Rt△FEG中,tanEGF=
=
可得∠EGF=
,故所求二面角的大小为θ=
所以AD∥平面BCS,
从而A点到平面BCS的距离等于D点到平面BCS的距离.
因为平面CSD⊥平面ABCD,AD⊥CD,
故AD⊥平面CSD,从而AD⊥SD,
由AD∥BC,得BC⊥DS,又由CS⊥DS知DS⊥平面BCS,
从而DS为点A到平面BCS的距离,
因此在Rt△ADS中DS=
| AS2-AD2 |
| 3-1 |
| 2 |
 (Ⅱ)如图,过E电作EG⊥CD,交CD于点G,
(Ⅱ)如图,过E电作EG⊥CD,交CD于点G,又过G点作GH⊥CD,交AB于H,
故∠EGH为二面角E-CD-A的平面角,
记为θ,过E点作EF∥BC,交CS于点F,连接GF,
因平面ABCD⊥平面CSD,GH⊥CD,
易知GH⊥GF,故θ=
| π |
| 2 |
由于E为BS边中点,故CF=
| 1 |
| 2 |
在Rt△CFE中,EF=
| CE2-CF2 |
| 2-1 |
因EF⊥平面CSD,又EG⊥CD
故由三垂线定理的逆定理得FG⊥CD,
从而又可得△CGF~△CSD,
因此
| GF |
| DS |
| CF |
| CD |
CD=
| CS2+SD2 |
| 4+2 |
| 6 |
故GF=
| CF |
| CD |
| 1 | ||
|
| 2 |
| 1 | ||
|
在Rt△FEG中,tanEGF=
| EF |
| FG |
| 3 |
可得∠EGF=
| π |
| 3 |
| π |
| 6 |
点评:本题主要考查了点到平面的距离,以及二面角的度量等有关知识,同时考查了计算能力、推理能力、以及转化与划归的思想,属于中档题.

练习册系列答案
相关题目
 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点. 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,